There are many misconceptions when it comes to the subject of mathematics. One of the most common myths I encounter is related to the way one approaches learning math.
The way one studies mathematics is fundamentally different than the way one would study other disciplines – particularly disciplines that are more related to recalling a set of facts (“knee bone’s connected to the thigh bone!”). Mathematics, I argue, is much more of a skill, comparable to playing the flute or learning to skateboard; it's like perfecting a jump shot in basketball or landing a pirouette. In other words, it is a process of skill mastery.
No one has ever learned piano by just reading a book and looking at videos without practice. Similarly, no mathematics teacher has ever recommended that you wait until the day before to “cramming” to get ready for the big test.
With these types of activities, you learn by doing. The books are there to help your transition from unconscious incompetence (“don’t know what you don’t know”) to conscious incompetence (“know what you need to learn”) to conscious competence (able to do the task with concentration) to unconscious competence (it’s automatic and just flows from you). Though tutors will be able to walk you through each of these conscious states -- from conscious incompetence to conscious competence -- the final stage ultimately allows the student to become independent.
One of the largest hurdles that a student must overcome when moving through these conscious stages is rooted in memorization. In the past, I've seen my students rely wholly on memorizing a mathematic equations, while neglecting the need to understand where the equation arises from.
As a simple example, consider the famous binomial equation, which gives the roots to a quadratic equation in one variable:
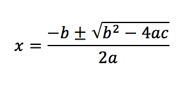
How many students know that this comes from completing the square? How many of those can actually derive it?
Similarly, consider the formula for derivative of sin(x). Do you now how to derive it from the definition of the derivative?
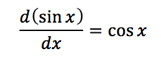
None of this is to say, as facetiously suggested by the title of this entry, that you shouldn’t memorize anything. But what is encouraged is that you take care to know where things come from and always make sure you can derive the results yourself. From that point, the memorization will take care of itself.
So the next time you come up against a commonly accepted result, see if you know where it came from and can actually derive it on your own. This will take you one step further on the path to true mathematical mastery.
Comments