If you’ve taken a high school physics class, you probably started by learning about position, velocity, and acceleration, ubiquitous concepts in physics that are also well-motivated by our daily life experiences. But soon after that, the course probably moved on to less familiar concepts, such as energy and simple harmonic oscillation modeled by masses on springs. At this point in the class it is natural to wonder: “how is any of this useful? I’ve never even seen a mass on a spring, so why are we spending a whole chapter focused on it?”
And yet, as you continue in your physics education, you’ll see the simple harmonic oscillator over and over again. From models studying the motion of a pendulum to the currents in electrical circuits, all the way down to the theories of the fundamental particles that comprise them, the same equations of motion that describe a mass on a spring show up in all of their grandeur. I’d like to discuss why the simple harmonic oscillator is at the core of so many different models in physics. In order to do so, bear with me as I recall a concept from calculus: the Taylor series.
The Taylor series is a way of writing any well-behaved function as a polynomial – a sum of various powers of x. Calculus teaches us that functions can be approximated by a line if we calculate their derivative and use this as the slope of that line. For values of x near the point where the line is tangent to the curve described by y = f(x), this is a good approximation, but it quickly becomes worse as the two curves diverge. We can improve this approximation, making it diverge less, by instead using a parabola or, even better, a cubic or higher-degree polynomial.
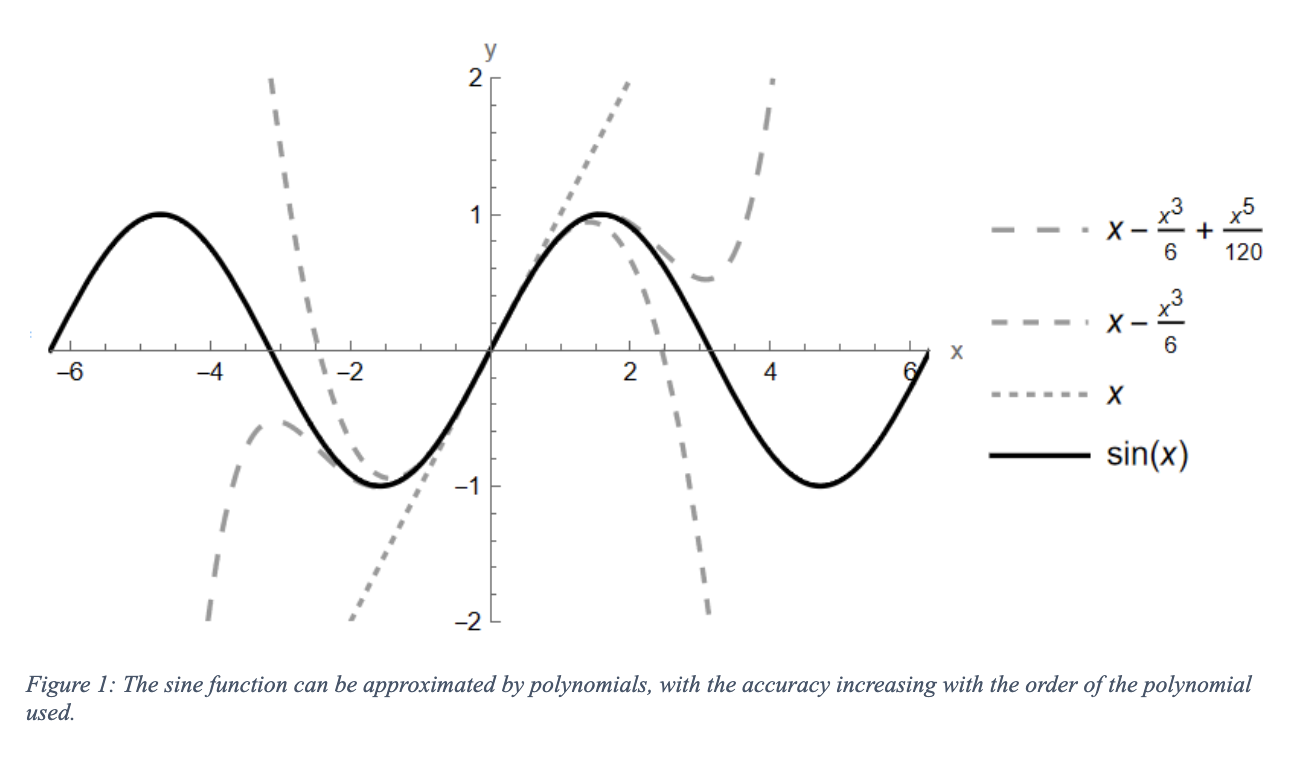
In physics, this is extremely useful whenever it is difficult to consider a problem exactly – in these cases we use a Taylor series (often using only a linear or quadratic approximation) to solve an approximate version of our problem. Making such an approximation is also well-motivated, because often the function we wish to approximate is the potential energy of a system, and typically systems do whatever they can to minimize this potential energy (balls roll down hills, springs push/pull masses back towards equilibrium, and radioactive nuclei decay over time). This means that often we only care about a small region around a local minimum of the potential energy function, and such a region can be well-approximated by a parabola.
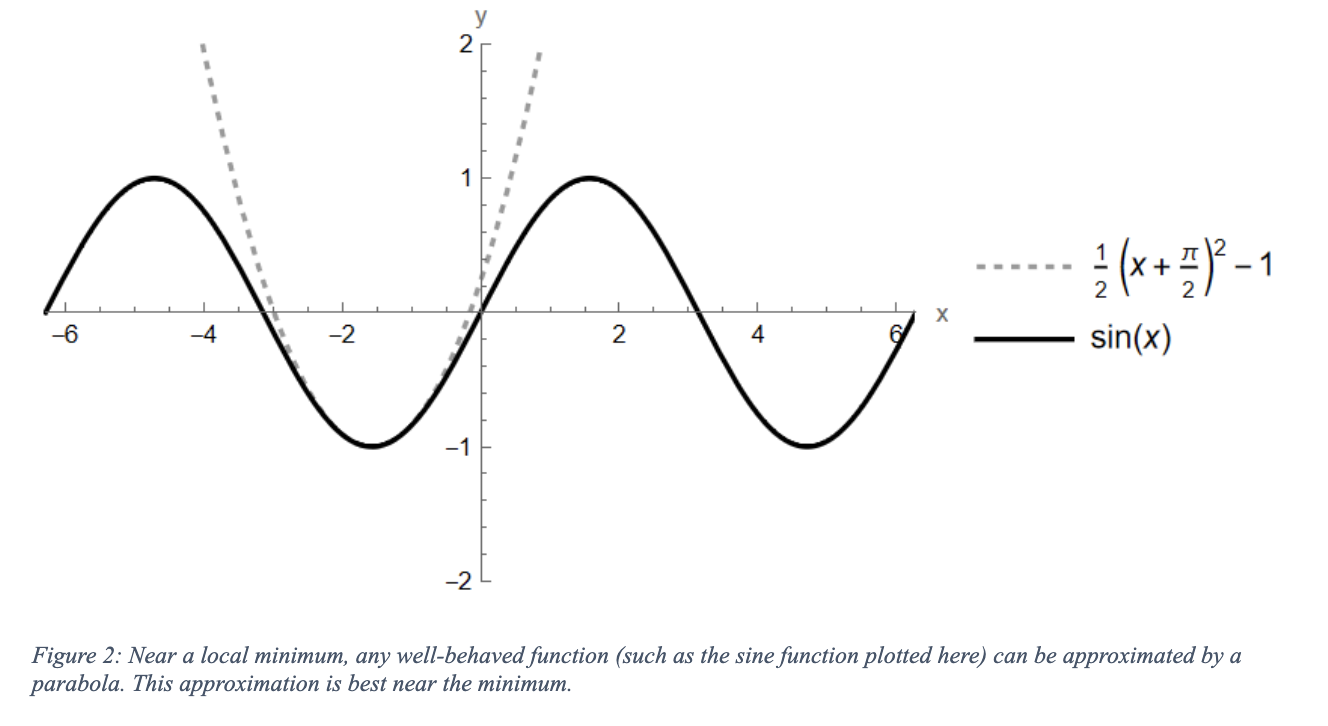
Why is it important that a parabola is a good approximation? Because a parabola is the potential energy curve for a simple harmonic oscillator, such as a mass on a spring! Recall the formula for spring potential energy:
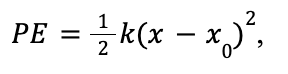
where k is the spring constant describing the stiffness of the spring and x0 is the equilibrium position where the spring exerts no force.
In summary, because physical systems tend to minimize their energy, the potential energy curves of a huge variety of systems can be well-approximated by the same curve that describes a simple harmonic oscillator. As a result, the behavior of these systems is described by the same equations of motion as a mass on a spring! The relevant variables might change – for example, instead of a mass oscillating back and forth, the equations could describe a string vibrating up and down, or a voltage rapidly switching from positive to negative, or even an electron jumping back and forth between two quantum states – but the underlying math is universal.
This is why high school physics courses teach about mass-spring systems. Although masses and springs themselves might not be very interesting, the simple harmonic motion they undergo provides a foundation for describing phenomena across all of physics. So the next time you’re trying to understand a physical system in terms of a potential energy curve, try to find an analogy with the simple harmonic oscillator. Eventually you’ll start seeing mass-spring systems everywhere!


Comments