In many science and engineering classes, units can be seen as an additional step that needs to be taken into consideration when completing a problem. In some problems on the Fundamental Engineering exam, mismatched units are intentionally used in an attempt to confuse students and measure their understanding of key concepts. Nonetheless, units hold critical information about the values in the problem and how they interact. If you can understand how units are functioning in a problem, you can unlock helpful hints to solving that problem!
1. How Dimensional Analysis can be used
Through the application of dimensional analysis, units can provide important hints about how to solve a problem. As an example, let’s look at the following physics problem taken from NCEES’s 2015 Fundamentals of Engineering sample questions [1]:
 This problem provides three types of units: N/mm, N, and mm. It asked us to solve for the force required (N), while providing us with the spring constant (N/mm) and two separate lengths (mm). To solve for the required force, we must somehow get Newtons using N/mm, and mm. The simplest form of doing this is as follows:
This problem provides three types of units: N/mm, N, and mm. It asked us to solve for the force required (N), while providing us with the spring constant (N/mm) and two separate lengths (mm). To solve for the required force, we must somehow get Newtons using N/mm, and mm. The simplest form of doing this is as follows:
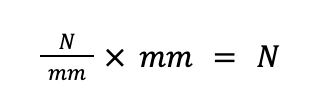 Therefore, we now know that we must multiply the spring constant by something with the units of mm. This knowledge rules out the possibilities of multiplying the two lengths together (which would result in units of mm2) or calculating a ratio of the lengths (which would result in a unit-less number). While it’s true that any linear combination of the two lengths will result in the required units of mm, two of the most reasonable ways to use these measurements in an equation that outputs N is to multiply spring constant by either the sum or the difference of the two measurements. This gives us the two following options:
Therefore, we now know that we must multiply the spring constant by something with the units of mm. This knowledge rules out the possibilities of multiplying the two lengths together (which would result in units of mm2) or calculating a ratio of the lengths (which would result in a unit-less number). While it’s true that any linear combination of the two lengths will result in the required units of mm, two of the most reasonable ways to use these measurements in an equation that outputs N is to multiply spring constant by either the sum or the difference of the two measurements. This gives us the two following options:
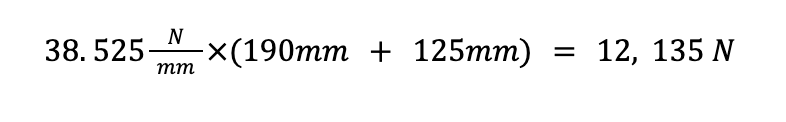 or
or
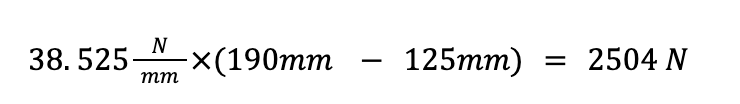
The first option can quickly be eliminated as it is not one of the possible answers leaving us to estimate the answer to be C: 2,500 N which happens to be the correct answer. We have now successfully solved a practice problem for the Fundamentals of Engineering exam with only dimensional analysis and without using any equations.
2. Broader Scope and Applications
While the example above is relatively naïve, it shows the power in using the information contained in units. This information is amplified as units get more and more complicated. It’s important to keep in mind that all units break down to five major physical quantities: mass (M), length (L), time (T), electrical current (I), and temperature (Θ). Below is a table of some common units in engineering and physics and how they break down.
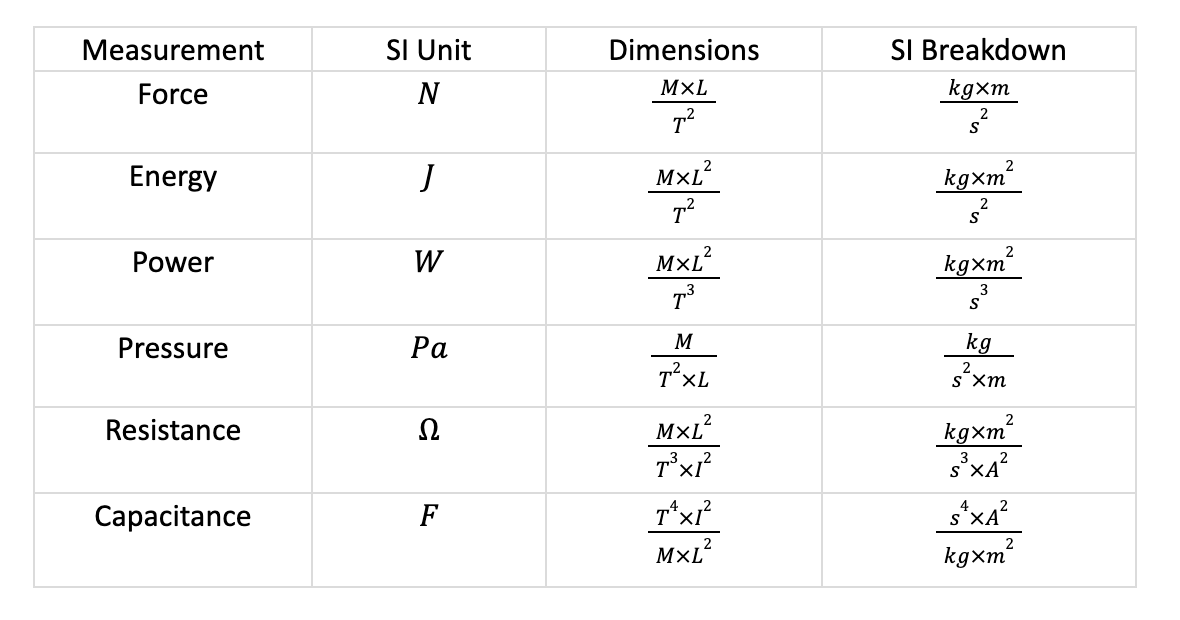 This information allows us to break down any coefficient into its fundamental units and glean the maximum amount of information contained in those units. Take for example thermal conductivity k, a material property essential in many heat transfer calculations.
This information allows us to break down any coefficient into its fundamental units and glean the maximum amount of information contained in those units. Take for example thermal conductivity k, a material property essential in many heat transfer calculations.
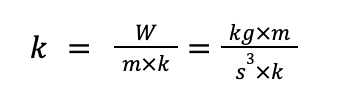 This breakdown hints at which values in a given problem might need to be multiplied or divided by thermal conductivity to get the desired output. While it’s unrealistic to expect to solve all problems simply from breaking down the units of the provided values, dimensional analysis is a powerful tool especially when combined with other knowledge. Specifically, it can give you an idea of what you need to do with your values before applying an equation to them. Many engineering classes and tests provide relevant equations. By analyzing the output dimensions of that equation, you can quickly eliminate many incorrect equations for that specific problem. Admittedly, there is no guarantee that your answer is right just because your units workout, however, it is a guarantee that your answer is incorrect if your units do not work out.
This breakdown hints at which values in a given problem might need to be multiplied or divided by thermal conductivity to get the desired output. While it’s unrealistic to expect to solve all problems simply from breaking down the units of the provided values, dimensional analysis is a powerful tool especially when combined with other knowledge. Specifically, it can give you an idea of what you need to do with your values before applying an equation to them. Many engineering classes and tests provide relevant equations. By analyzing the output dimensions of that equation, you can quickly eliminate many incorrect equations for that specific problem. Admittedly, there is no guarantee that your answer is right just because your units workout, however, it is a guarantee that your answer is incorrect if your units do not work out.
Conclusion
One of the most important pieces of information provided in physics and engineering problems is the units of the given and desired values. Being able to quickly breakdown and understand the interactions of different units take much practice but is essential to becoming a proficient engineer.
Sources
[1] Fundamentals of Engineering Sample Questions, National Council of Examiners For Engineering and Surveying, 2015. https://www.engineeringonline.ncsu.edu/wp-content/uploads/sites/23/2018/02/FE-Sample-Questions-Book_2015.pdf

Comments