What is a determinant?

This is a blog post about understanding linear maps and a special number associated to them called the determinant. A linear map f from Rⁿ (n-dimensional Euclidian space) to R^m (m-dimensional Euclidian space) is any map which satisfies the following properties:

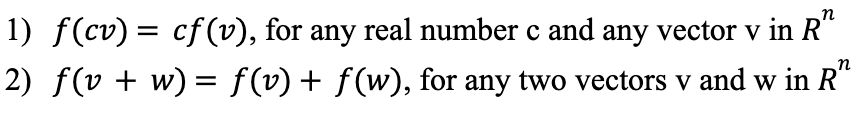
We are sometimes taught to think of a linear map as a function defined using coordinates. For example, here is one linear map:

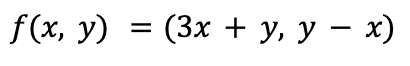Or we are taught to think of a linear map as a matrix. Here is the matrix that corresponds to the linear map above:

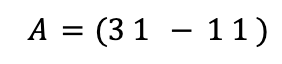
A corresponds to f because for any vector v in R² we have:

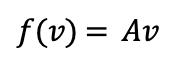
Another important way of understanding linear maps, which I want to introduce in this blog post, is through pictures. Here is a picture that helps us understand the map f above.

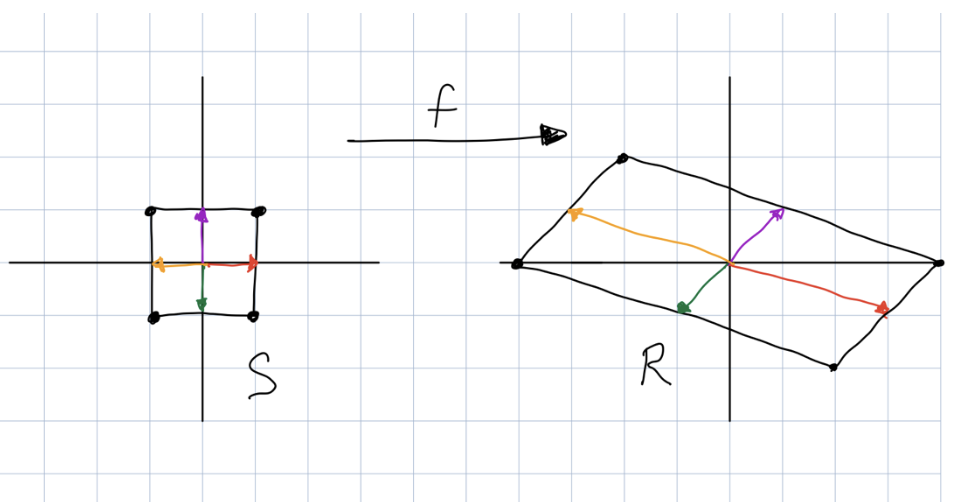Figure 1. Grid drawn at scale 1.

If we call the set of points inside the square on the left, S, and we call the set of points inside the parallelogram on the right, R, then the image of S under the map f is R. In other words:

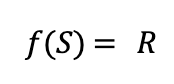
The picture also shows us how the axes of S, which are drawn in different colors, are mapped under S to the axes of R. For instance, the purple vector on the left is 0,1 and it gets mapped to the purple vector on the right, which is 1,1.

In higher dimensions, we can no longer draw pictures and we’ll need to rely on the coordinate or matrix representations of linear maps, but we can still get a lot of intuition from looking at these kinds of pictures in 2 and 3 dimensions.

Now let’s introduce the determinant.

The determinant is a number associated to a linear whose range and domain have the same dimension.

Suppose f is any linear map from Rⁿ to Rⁿ. The determinant of f is a real number, which we denote by det (f) , and is defined by the following equation:

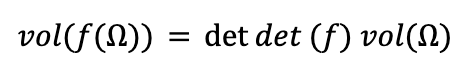
where Ω is any region in Rⁿ of positive volume, and vol(Ω) stands for the n-dimensional volume of Ω.

It should be surprising that there is one number that makes this equation true no matter which region we choose!

For the interested reader, we’ll explain why this is so in the appendix, but for now let’s just take this fact for granted.

An example:

Let’s try this definition out on our previous example. Choose Ω to be our square S from Figure 1. The domain and range are 2-dimensional, so n=2 and vol(S) is just the area of S which is 4.

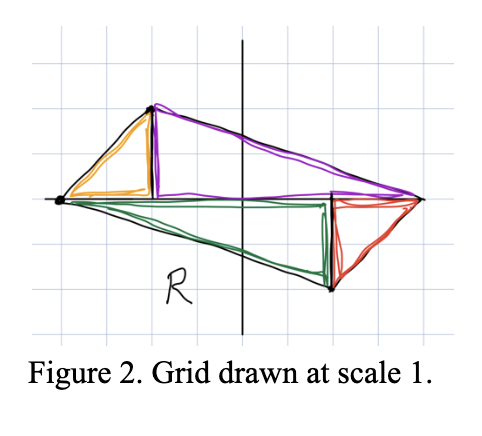
We can find the area of f(S), which we saw is R, by adding up the areas of the different colored triangles in Figure 2.

vol(purple triangle) = vol(green triangle) = 6

vol(red triangle) = vol(orange triangle) = 2

Adding all these up, we get vol(R) = 16, and so: vol(f(S)) = 4vol(S)

Finally, from our definition of the determinant we see that f = 4.

A surprising property of determinants...

In this section, we’ll discuss a surprising property of determinants. Suppose we have another linear map g. We let g º f stand for the composition of g and f. In other words,

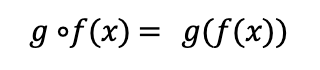
What can we say about det(g º f)? From our definition of the determinant we have,

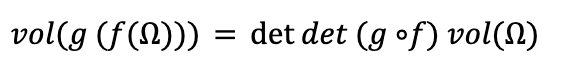
But since we are free to choose f(Ω) as the region in our definition for the determinant of g, we get that:

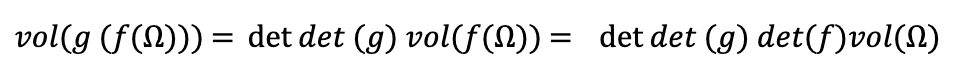
Putting the two together we find,

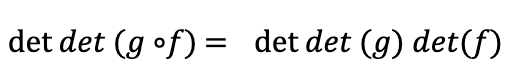
If g corresponds to a matrix B and f corresponds to a matrix A, this equation becomes

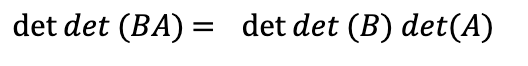
So, when we compose matrices, the determinants just multiply!

A formula for the determinant of a 2x2 matrix

A formula we often learn first in a lecture about determinants is

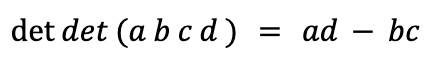
Let’s see how we might derive this from the definition we have.

The matrix above corresponds to the map:

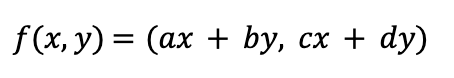Here is a picture for how the map f transforms the region Ω = square at the origin with side-length 1.

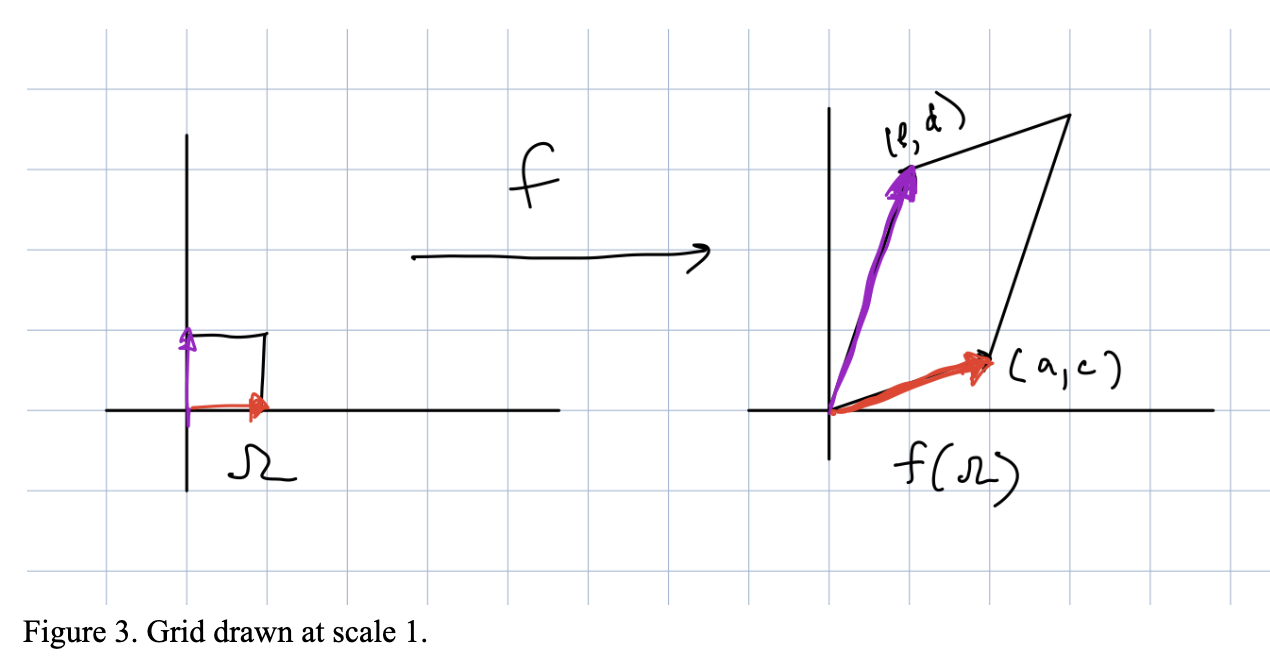
To find det⁡(f) we need to compute vol(f(Ω)). To do this take a look at the following picture.

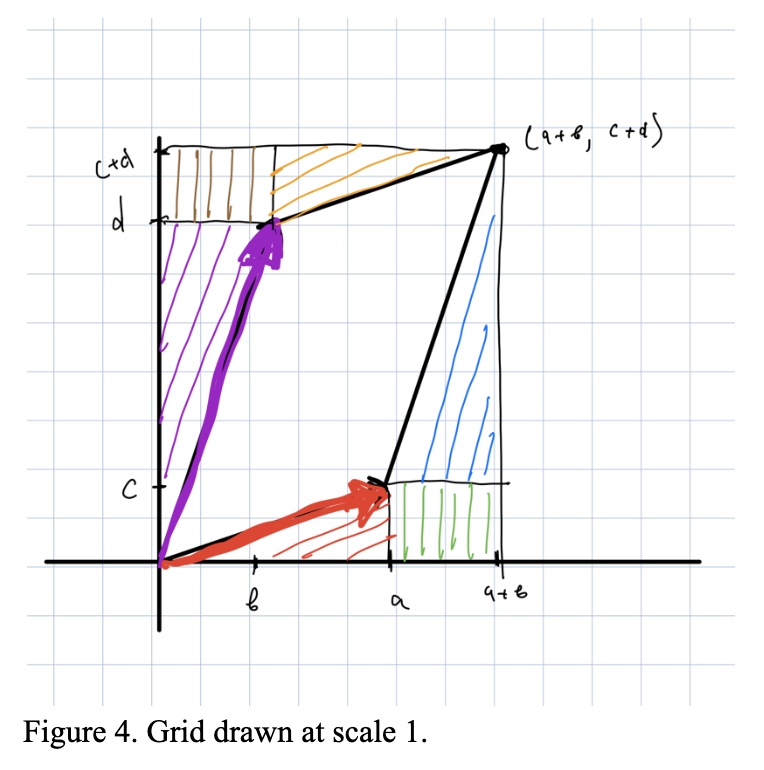
vol(f(Ω)) is just the area of the rectangle with sides a+b and c+d, minus the area of all the colored regions in Figure 4. So, we just need to compute the areas of the colored regions.

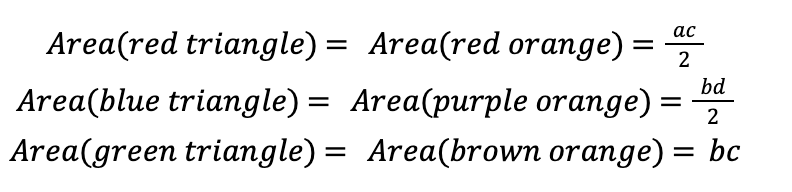Putting this together we have,

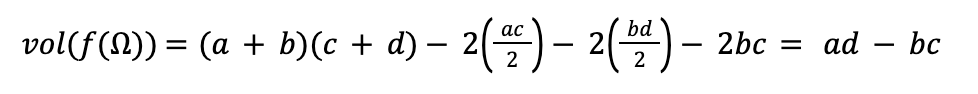
And we get our formula:

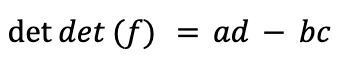
Appendix

In this appendix, we discuss the surprising fact mentioned after the definition of the determinant. It’s a more advanced section and we’ll assume some familiarity with the concept of a proof as well as the concept of a limit. In particular, we’ll prove the following.

Theorem: Suppose f is any linear map from R² to R². Then there is a unique real number called det⁡(f) for which the following equation is true,

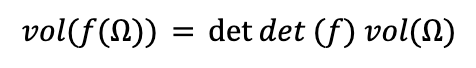
whenever Ω is a region in R² of positive volume.

(The statement is true if R² is replaced with Rⁿ and the proof is almost exactly the same.)

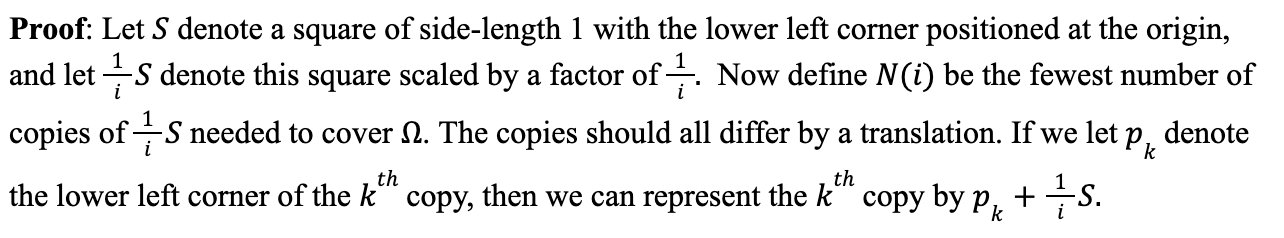
Notice that we have:

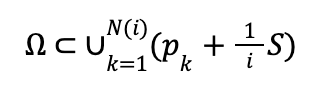
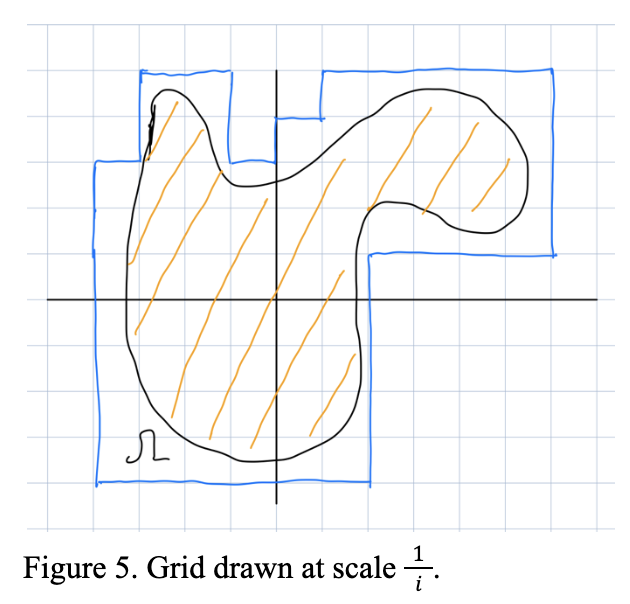
For example, in Figure 5, the region shaded in orange is and the blue line outlines all the copies of the square (1/i)S that cover it. The copies of S can be visualized as the individual cells from the grid in Figure 5.

Now notice that as i goes to infinity, the approximation of our region by the copies of S(i) gets better and better. In particular, as i goes to infinity we see that vol(S(i))N(i) approaches vol(Ω).

From the additivity and scaling property of linear maps we can see that:

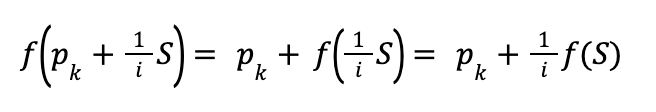
And from this it follows that:

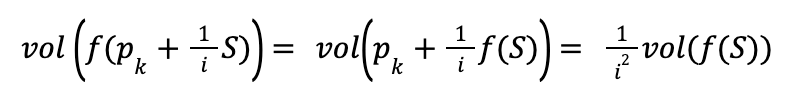
Notice that we have shown that this volume doesn’t depend on k. Now see let’s what this says about vol(f(Ω)). As i goes to infinity, our approximation of Ω by copies of (1/i)S gets better and better. So, we get the following limit:

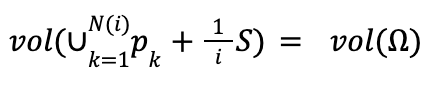
Since all the copies are disjoint we have

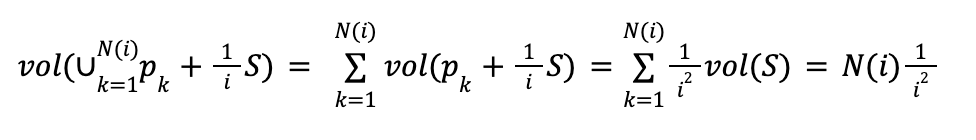
Combing this we the above limit we get,

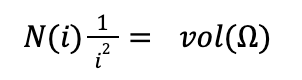
Notice also that, as i goes to infinity, our approximation of f(Ω) by the images of our copies under f, gets better and better. From this we get the following limit

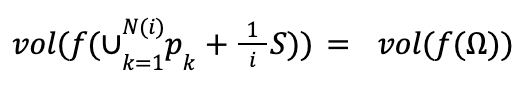
Since all the copies are disjoint we have

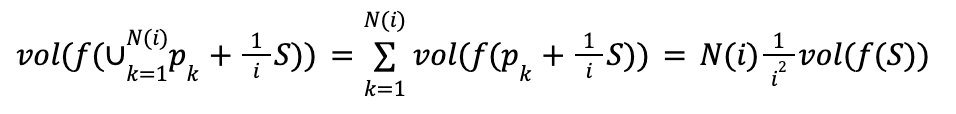
Putting everything together we get

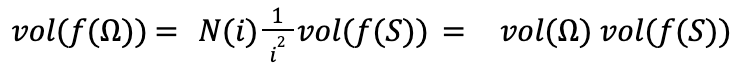
Which finishes our proof.