What is implicit differentiation and how does it work?

One topic that seemed a bit mysterious and magic to me when I first learned calculus was implicit differentiation. In this post, we’ll start by reviewing some examples of implicit differentiation and then discuss why implicit differentiation works.

An example

In an implicit differentiation problem, you’re generally given an equation involving x and y such as

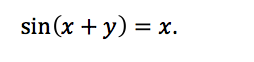
Then, you’re asked to find the derivative of y with respect to x. One way to do this is to solve for y with respect to x and then take the derivative normally. Another way is via implicit differentiation by differentiating both sides with respect to x.

Doing so, we get:

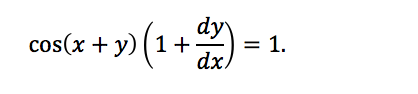
What happened here? On the right-hand side, the derivative of x with respect to x is just 1. Using the chain rule on the left-hand side, the derivative of sin(x + y) is cos(x + 1) • (d/dx)(x + y). The derivative of x with respect to x is 1, while the derivative of y with respect to x is unknown, so we just leave it as dy/dx.

Then, we solve for dy/dx to get that:

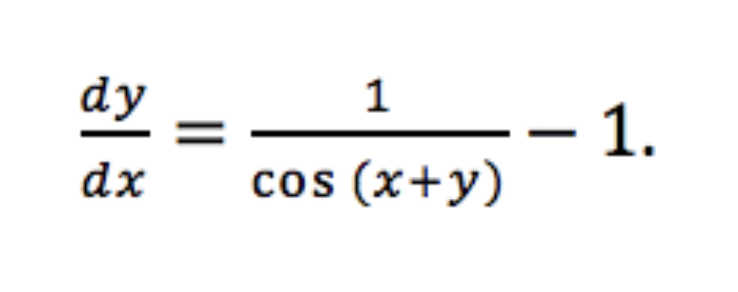
When might we want to use implicit differentiation? Implicit differentiation is super useful when you want to find the derivative dy/dx, but x and y are not related in a simple manner like y = ƒ(x). Rather, x and y might be related by some more complicated expression like sin(x + y) = x where it might be tricky to write y in terms of x.

This is the prime time to use implicit differentiation because it allows us to go straight to differentiating both sides rather than worry about isolating y, which could be difficult.

What is the intuition behind implicit differentiation?

Let’s explore the idea behind implicit differentiation via an example. Suppose that we have the equation of a circle of radius 5,

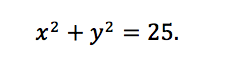
In other words, we can take the derivatives of both sides with respect to x and these derivatives must always be the same.

When we take (d/dx)(x² + y²), we're seeing our first glimpses of multivariable calculus. That is, we're thinking of x² + y² as a function of both x and y and taking the derivative of this multivariable function with respect to x. In other words, we are asking: how does the function x² + y² change as we vary x?

The one complicating factor is that we also have to remember that y has a dependence on x when we take the derivative. Let's try taking this derivative. Breaking up x² + y² into parts, we see by ordinary differentiation that take (d/dx)(x²) = 2x. To find (d/dx)(y²), we need to remember that y is secretly a function of x. This is like writing y = ƒ(x) and finding the derivative of (ƒ(x))² with the chain rule to be 2(ƒ(x))ƒ'(x). Thus, we get the following:

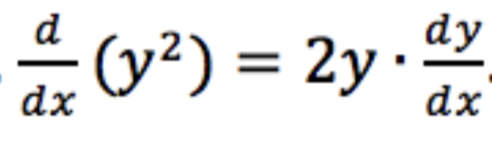
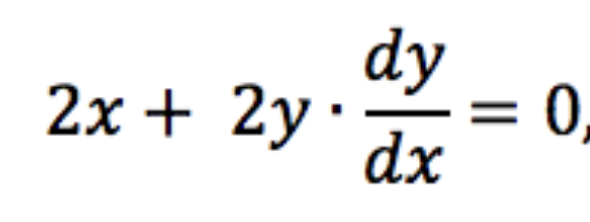
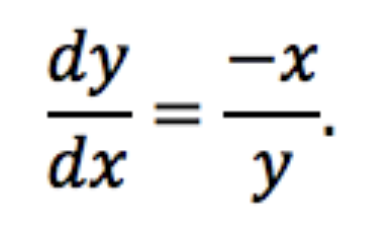
So if we wanted the slope of the tangent line of the circle of radius 5 at the point (3,4) for example, we could use the derivative that we just found to get that the slope of the tangent line there is -4/3.

In conclusion

Implicit differentiation is a super important tool when finding derivatives when x and y are related not by y=f(x) but by a more complicated equation. By remembering that two sides of an equation are always equal and therefore their derivatives with respect to x must be equation, and remembering that y depends on x, we can carefully take derivatives of both sides with respect to x, rearrange, and then solve for

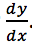
This allows us to find derivatives even in cases when it’s hard to write y as a function of x.