
Welcome back to our series of posts on gaining an intuitive grasp on the basics of electricity and magnetism.
In the first post, we looked at the physical reasoning behind Coulomb’s law and learned why the electric field of a point charge falls off by 1/r2. In the second post, we explored the somewhat deceptive but mathematically useful parallels between Coulomb’s law, which gives electric field due to a point charge, and the Biot-Savart law, which gives the magnetic field due to an infinitesimal bit of current.
Let’s use these two concepts, the 1/r2 scaling of the electric field due to a point charge and the convenient symmetry between electric and magnetic fields, as jumping-off points. In this post, we will look at how the expressions for the electric and magnetic field change when you consider simple geometries like the infinite wire or the infinite plane.
Recap: Coulomb’s law and the Biot-Savart law
Let’s look again at Coulomb’s law and the Biot-Savart law:
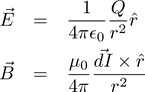
For this post, though, we will ignore the direction of the field and just concentrate on finding the magnitude. Stripped of the fields’ directions, the two expressions look even more alike:
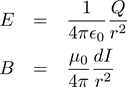
Note that you would need to take the geometry into account when you actually do the math to find the field magnitudes – for example, the parallel component of the electric field created by one point in an infinite plane of charge will always be cancelled out by the parallel component of another point, leaving only the perpendicular component – but we are skipping over the math for now.
There are several website that will show you how to calculate the following expressions yourself using Coulomb’s law and the Biot-Savart law or, more easily, Gauss’s law and Ampère’s law, but we will take the luxury of skipping to the results. The point of our discussion is not to show how the math works out, but rather to explain why the answer the math gives us should make intuitive sense.
Two common geometries: the infinite wire and infinite plane
Let’s consider two of the most common geometries that pop up again and again in introductory high school or college physics classes. They are also favorites on standardized tests like the physics SAT II or physics GRE.
The first geometry is the infinitely long wire, which either has a static charge density per unit length λ or carries a constant current I. We want to find the electric or magnetic field, respectively, at some radius r from the wire.
The second geometry is the infinite plane of charge or current. In this case, the plane of charge is characterized by a charge density per unit area σ and the plane of current is characterized by a current density per cross-sectional length K. The current density might be difficult to grasp intuitively, so imagine unrolling a roll of aluminum foil and connecting the two ends to a battery. If, say, 1.2 A flows through the 12-inch-wide sheet, then K = 1.2 A / 12 in = 0.1 A/in. If you prefer, you can imagine a flat ribbon of wires each carrying a current I; if the ribbon has N wires per inch of width, then K = NI.
In this geometry, we usually want to find the field at some height above the sheet. Usually, you might use h or d to symbolize this height, but we will use r here to be consistent with the equations above.
After slogging through the appropriate integrals, we would come to these results:
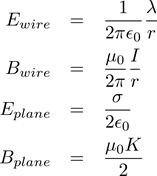
Beautiful symmetry between E and B
The first thing you might notice is the beautiful symmetry between the two sets of equations. Just as Coulomb’s law and the Biot-Savart law look precisely the same if you change charge to current and 1/ε0 to μ0, the equations for E turn into the equations for B under the same transformations. If you think about it, this is how it must be; the calculus doesn’t care what physical thing you are trying to calculate.
Because of this symmetry, we will use continue to discuss these results by considering only what happens with the electric field. The exact same reasoning will then also apply to the magnetic fields.
Different scalings with r
Next, you might notice that electric fields in the cases of the two geometries and the point charge scale differently with r:
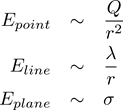
There’s a clear pattern here that’s easy to remember: for a plane, a two-dimensional geometry, r doesn’t matter or, in other words, the field scales as 1/r0. For a line, a one-dimensional geometry, the field scales as 1/r1. For a point, which could be considered a zero-dimensional geometry (no length, width, or height; just a point), the field scales as 1/r2. It seems, then, that for every dimension you add, you lose a power of r in the denominator. This is very handy for remembering these formulae, but where does this pattern come from physically?
Dimensional analysis: helpful but perhaps not illuminating
We could explain this pattern by noting that the way we measure charge is different for the point, line, and plane. Q is a measure of charge, whereas λ is charge density per unit length and σ is charge per unit area. Since λ and σ have units of 1/length and 1/length2 built in, we need to get rid of one and two factors of 1/r, respectively, to make the units match.
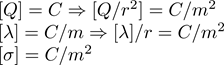
Similarly, for the magnetic field equations, remember that dI has units of current*length, I is current, and K has units of current/length.
This argument makes sense, but it’s a bit dry for my taste. Is there a more physical, intuitive answer?
A physical explanation
To get a physical intuition for why these different geometries scale differently with r, let’s consider the case of an infinite line of positive charge in more detail. Imagine the line is horizontal on the x-axis and we put our test charge at a height r on the y-axis. Every piece of charge in the line will contribute to the electric field at the point (0,r), but some will contribute more than others. A piece of charge that is far off to the right (x >> r) will contribute a small field that points almost horizontally to the left; this contribution will be almost entirely cancelled by the contribution from a charge that is similarly far off to the left, which creates a field pointing to the right. Therefore, all points that are far away to either side simply do not contribute significantly to the net field at (0,r) and we can ignore them.
We can then ask ourselves how close a piece of charge needs to be to the origin before it contributes significantly to the net field. That is, how close does it need to be before it creates a field at (0,r) that has a significant vertical component, which will not be cancelled out by some other piece of charge, rather than a mostly horizontal field, which will be cancelled?
I hope that this intentionally vague question reminds you of the story that kicked off this series on physical intuition, my anecdote of the square of charge. Reasoning along the same lines that my professor had in my story, we realize that a piece of charge needs to be closer to the origin than r (i.e. |x| < r) to contribute significantly!
This explains the 1/r scaling exactly! If you have ~r pieces of charge that each contribute a field that falls off as 1/r2, then the total field scales as r*1/r2 = 1/r.
The same reasoning applies to the infinite plane. Putting the test charge at a height r above the origin, then we can reason that a piece of charge in the plane needs to be within a circle of radius r around the origin to contribute significantly. Since there are ~r2 pieces of charge within this circle, then the total field scales as r2*1/r2 = 1. In other words, the field above an infinite plane is independent of r!
Independent of r? How is that possible?!
If you are disturbed by the thought that the electric field above an infinite plane of charge (or, for that matter, the magnetic field above an infinite plane of current) does not depend on how far from the plane you are, then that is good. You are listening to your intuition as it rebels against a fairly counter-intuitive fact.
I would encourage you to read the story I mentioned, about determining the height at which a square of charge is significantly different from an infinite plane of charge. I would also encourage you to imagine flying in an airplane above a perfectly smooth sea on a perfectly cloudless day, the kind of idealization in which we physicists delight. With no size references – no waves or ships, only the sea stretching blue to the horizon – how would you know how high you are? Would you know the difference between flying 500 feet or 5 miles above the surface, and isn’t the concept the same for fields above a plane of charge or current?
Two caveats
This picture is great for remembering how the fields scale with r for different geometries, but it misses two other important things. First, the expressions for the fields due to the infinite line and plane are missing factors of 2 and π compared to Coulomb’s law and the Biot-Savart law. Our physical argument doesn’t catch those factors, but it wasn’t meant to. In fact, I cavalierly threw out these numeric factors during the course of the argument because we shouldn’t make the mistake of thinking that this intuitive method is more precise than it actually is: we ignored several subtleties in order to get to the underlying general concept. You really need to do the math in order to get the precise results I quoted, with all of their correct numeric factors.
Second, we were dealing only with the magnitude of the fields, not their directions. Although we invoked geometry to explain why the contributions from pieces of charge that are far away from the origin cancel each other, nothing we’ve said determines in a robust way the direction in which the field should point. In the next post, we will discuss how you can intuit the fields’ directions in addition to their magnitudes.
I hope if you’ve made it to the end of this rather lengthy post, that you will come away with an appreciation for the beauty of how these equations interrelate. The many equations that you learn as you begin E+M do not look alike in order to deliberately confuse you; they look alike because their underlying concepts are tied together at a fundamental level. If you can use your physical intuition to catch a glimpse of these sometimes hidden ties, then you will be a better physics student for having done so.

Comments