
Your first high school or college physics course in electricity and magnetism can often be a daunting experience.
Coming fresh off your recent mastery of mechanics – balls, springs, strings, and everything Newton – you might be struck by the suddenly more abstract nature of the material. Ropes, pulleys, and wedges are easy to visualize, but magnetic fields, electric potentials, and point charges require more of an imaginative departure from the everyday tactile world.
To complicate matters, a list of the crucial equations you will encounter in the beginning of the course reads like the dramatis personae of an Emily Brönte novel – itself another potentially bracing high school experience. Each equation is distinct, with its own derivation and applications, but many of them feature most of the same letters arranged in roughly the same form, and the precise relationships between the equations can be difficult to keep straight on your first encounter.
All of those similarities, however, can be very useful once we develop the physical intuition helps us put each equation in its proper place.
Over the next few posts, I will share my wisdom as a physics tutor: let’s try to develop some intuition for why the equations of E+M are what they are.
Coulomb’s law – why 1/r2?
Specifically, let’s start with Coulomb’s law. In general, Coulomb’s law states that the electric field generated by a point charge q is given by
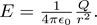
Why 1/r2, and where does the 4π come from? It is very easy to confuse the 1/r2 dependence of the electric field with the 1/r dependence of the electric potential, so let’s examine the physical reasoning behind the equations.
Intuitively, it’s easiest to imagine that point charge emanates an electric field, much like the sun emanates light. This is, in fact, the very essence of Gauss’s law but, since you might not encounter the wonder of Maxwell’s equations in this first E+M course, we will be satisfied with paraphrasing Herr Gauss for now. The sun emanates a fixed amount of light, called the flux, which is radiated evenly in all directions. We can imagine that light spread evenly over a sphere of radius r that surrounds the sun. Since the sphere has a surface area of 4πr2 over which the sunlight is spread, the intensity ( = flux/area) at any point on the sphere is proportional to 1/4πr2.
You can feel this effect at work as you sit around a blazing campfire at night. Standing outside the circle of people, your body takes up a relatively small portion of the area (more correctly, the solid angle) into which the fire is radiating heat and you are chilly. As you lean in, though, your face takes up a larger and larger portion of the surface of a smaller and smaller sphere, so the intensity of the heat on your face increases and you begin to feel quite toasty.
What Gauss’s law says is that total electric flux emanating from a point charge is given by Q/ε0, where Q is the charge of the point charge and ε0 is the permittivity of free space, a physical constant. By analogy with the sun example, the electric field intensity at any point a distance r from the charge is
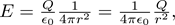
which gives us Coulomb's law.
Why 1/r for the electric potential?
Once we know Coulomb’s law, the electric potential is easy to derive. To find the electric potential at any point, we simply need to know the amount of energy needed to bring a test charge q to that point from a point infinitely far away, at which we define U=0:
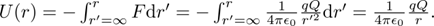
The potential energy of the test charge can depend on q, but we would like to define the potential created by the charge Q as being independent of whatever test charge we use to find the energy. Thus, we define the familiar potential
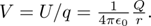
Intuitively, it is useful to remember that the force is proportional to E and scales as 1/r2 (think of the electric flux spread over the surface of the sphere), and you give a particle energy by moving through some distance against the force of the electric field, so by dimensional analysis, V scales as 1/r2*r = 1/r.
Extending beyond a point charge
How do these equations change if we consider other standard distributions of charge, like the infinite line and infinite plane? What if we set these charges in motion so that they create a magnetic field in addition to an electric field?

Comments