
Welcome back to our series on exploring the role of analogy in science. Last time, the Physics Tutor talked broadly about how reasoning by analogy – extending specific reasoning from one context to a new context, or forging new logical ties between systems that were thought to be unrelated – is important to the advancement of science.
In this post, let’s take a more practical look at analogy. How can it be useful to you in your own high school or college physics career? Occasionally, you will notice patterns emerging as you study several different topics, motifs in the equations. If we pay attention to the patterns, can we arrive at some insight about some interesting physical property that underlies the pattern we see? Let’s find out!
Let’s start with high school-level mechanics
Today, let’s talk energy. The three forms of energy you probably remember from your first semester of physics are kinetic energy, the potential energy of a mass on a spring, and gravitational potential energy:
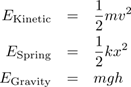
Let’s put aside that outlier gravity for a moment and look at the expressions for kinetic energy and the spring’s potential energy. You’ve probably noticed that the two expressions look very similar, and I expect you’ve used that fact to your advantage while studying for exams. Is this similarity a nice and convenient coincidence, or does it hint at a more fundamental pattern?
A basic example: mass on a spring
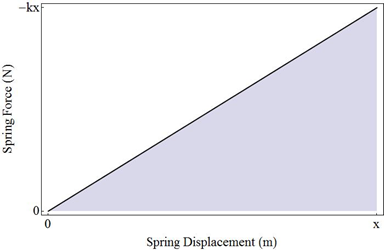
First, let’s find out where the energy of a spring comes from. There are two important characteristics of the spring’s force that we need to understand. First, the spring’s force is conservative. When you push on a mass attached to the spring, you compress the spring and give it potential energy. When you release the spring, it makes the mass accelerate outward. If we make the usual assumption that there is no friction, then energy is conserved; all of the energy you give the spring as potential energy is eventually given to the mass as kinetic energy.
Second, the spring’s force is linear. The force with which you push on the spring is linearly proportional to the distance you’ve already compressed the spring. This is expressed by the familiar equation
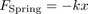
So how do we find the spring’s potential energy? In general, when you push against a force, you are spending energy to do so. If the force you apply is constant, then the energy you spend is given by the force you apply times the distance over which you apply it:
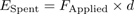
If the force is conservative, then the energy you spend is transferred to potential energy; like money that you put in a bank, you expect to be able to get all of that potential energy out again in the form of kinetic energy. The potential energy you build up is then exactly the same as the energy you spend:
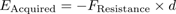
The negative sign comes from the fact that the FResistanceand d point in opposite directions, since you are pushing against some resistance.
What if the force you apply is not constant, though? The spring is easy to push at first, then resists more and more as it is compressed. You spend very little work pushing it the first inch, and a good deal of work pushing it the last. In this case, you just need to add up all the infinitesimal bits of energy you spend to push the spring in by infinitesimal distances. The simple product turns into an integral, giving the spring’s potential energy:
If you’re not familiar with calculus, then you can imagine a graph that plots the force exerted by the spring (negative, because we define the direction of compression as positive) as a function of the spring’s compression. If you calculate the area of the shaded region under the curve (it’s just a triangle!), you again get ½ kx2!
So why this insistence on the math? The mass on a spring is such a canonical example that I want you to be very familiar with how it works, and where the expression for the potential energy comes from – the k comes in because it determines how stiff the spring is, one factor of x comes in because it determines how far you push the spring, the other factor of x comes from the fact that the spring force is proportional to compression, and the ½ comes from the fact that you’re not pushing against the spring’s full kx force the entire time.
What about kinetic energy?
Now we understand how conservative linear forces work, but how does the spring relate to kinetic energy? For that matter, where does the kinetic energy formula come from? I’m going to explain using a calculus-based approach, but you don’t need to follow the math in order to understand the underlying concept (a non-calculus explanation is also given here). Essentially, we can perform the same “force times distance” integral using the generic F=ma and play some calculus tricks to find the answer:
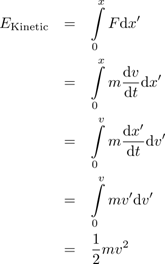
Even if you haven’t learned calculus yet, I want you to look closely at the last two lines. They look very similar to the last two lines of our calculation of the spring’s potential energy, don’t they? Let’s think about what happens in the two cases.
In the first case, we want to compress the spring by tiny increments until we’ve compressed it a distance x, but the more we compress the spring, the more the spring resists. The degree to which the spring resists our pushing is characterized by the spring constant k. You can see 0 (our initial compression), x (our final compression), and kx’ (the spring’s resistance force at any point) right there in the integral.
In the second case, we want to give our mass tiny boosts until it reaches a velocity v. The crucial point, although it might not be immediately obvious, is that it takes more energy to accelerate a moving object than a still object. Think about the energy required to push a shopping care into motion compared to the energy required to run behind a moving shopping cart and give it an additional boost. The more groceries you have in the cart (the more massive the object), the more power you need to use. We can see that adding tiny bits of velocity to our moving object is exactly analogous to adding tiny bits of compression to our spring, where m and k characterize how much harder we need to work as the object gains velocity or the spring is compressed. Therefore, the result is the same, with the final velocity v taking the place of the final compression x and the inertial mass m taking the place of the spring constant k.
Now, let’s think about why the equation for the gravitational potential energy does not follow the same pattern. What happens to the force of gravity as you lift an object higher and higher? Does it make sense, then, that you only get one factor of h and not two?
So these two equations look the same. Why should I care?
That’s a fair point. I’ve taken two equations that you probably memorized long ago and subjected you to an ungodly number of integral signs in order to explain their common origins. Why should we go through the effort to understand such simple concepts in such close detail?
The answer is that this basic concept – that position and momentum are intimately linked – is ubiquitous throughout physics. Think about a mass oscillating on a spring. The mass has only potential energy when it turns around at the limits of its motion, and has only kinetic energy in the middle of its range when the spring is completely relaxed. Displacement gives way to momentum, which in turn gives way to displacement again; energy flows seamlessly back and forth between potential and kinetic.
We can go trace this conceptual thread far beyond high school-level mechanics, though. The circuits in your cell phone; electric and magnetic fields; quantum mechanical light; photons, phonons, and the very cutting edge in light-matter interaction – all of these are, on some level, just different ways of thinking about a mass on a spring.
Tune in next time, when we’ll start to see how far our understanding of this simple analogy can take us!
Comments