
Ever lost points on a test because you forgot to write the units?
Rightfully so! Numbers have no meaning without their units of measurement. Two can be greater than 12. Three can equal one. This is all dependent on the unit of measurement being used. In your general chemistry class, you will encounter measurements of all sorts. These measurements include time, length, mass, volume, and many more. Units of measurement are used to conceptualize the magnitude of these measurements. Gram, kilogram, pound, ounce, metric ton, stone, slug, microgram, atomic mass unit, carat… these are all units of measurement for mass alone. Why so many? Some units of measurement are more appropriate depending on what thing is being measured. Using an inappropriate unit of measurement may result in a number value that is too large or too small. When this happens, it becomes very difficult to wrap your head around the magnitude of the measurement.
Conversion factors and their use
A conversion factor is used to change the unit of measurement without changing its value. On your general chemistry exam formula sheet, you will see them as equalities where opposite sides of the equal sign are a given measurement expressed in different units:
1 inch = 2.54 centimeters
1 yard = 3 feet
1 foot = 12 inches
I’m sure that if you were asked to calculate the number of centimeters in four inches, you’d be able to calculate it with no problem. If one inch equals 2.54 centimeters, then four inches equals 4 times 2.54 centimeters. Easy. Some conversions are not this intuitive. Especially when they require more than one conversion factor to get to the unit of measurement you’re interested in. The factor-label method is a foolproof way to perform conversions.
The science behind the factor-label method
First things first, the conversion factor, initially given to you as an equality, needs to be written as a fraction. What side of the equal sign goes in the numerator and what side goes in the denominator? It depends! But we’ll get to that soon. For right now, what’s important to know is that both fraction possibilities, reciprocals of one another, are valid. Why is this?
Consider the conversion factor: 1 inch = 2.54 centimeters.
Two fractions can be made from this:
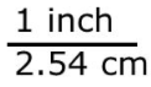
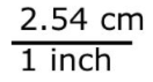
In both fractions, the numerator and denominator are equal quantities. Thus, these two fractions equal one another and both are equal to 1.
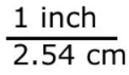
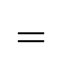
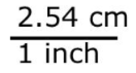

The name of the factor-label method game is to multiply the value you are given, unit of measurement included, by the conversion factor in fraction form. Remember how I said conversion factors do not change the value of a unit of measurement? The factor-label method endorses this. The fraction you are using to perform multiplication with is equal to 1! We all know any value multiplied by 1 is the same value. The only thing that will change is the unit of measurement.
So, let’s finally get into the nitty-gritty of the factor-label method. Your setup will always have the following pattern:



Recall that the fraction portion is your conversion factor and that it is equal to 1. We can now answer the question about which fraction we use since there will always be two possibilities. Your goal is the cancel out the unit of measurement you are no longer interested in. Whatever unit you are given to start with will guide what fraction you use. In other words, you want the unit you are given to start with to be in the denominator. In doing this, you will be left with the unit you want.

So, using the factor-label method, how many centimeters are in four inches?

When plugging this into the calculator, divide the product of all the values in the numerator by the product of all the values in the denominator. You can think of the 4 in the problem above as 4 over 1 to help you visualize how to multiply.
Some questions to ask before setting up:
- What units have I been given to start with?
- What units have I been told to find?
- What conversion factors have I been given to get from 1 to 2?
On a typical general chemistry exam formula sheet, you’ll find a plethora of conversion factors – some of which you won’t even need. As a rule of thumb, the conversion factors you will use will contain the units you have been given to start with and/or the units you have been told to find. Keeping this in mind will prevent you from being overwhelmed by the formula sheet.
The first conversion factor you use must have the units you have been given to start with because your first goal is to cancel that unit out. If the other unit in that conversion factor happens to be the units you have been told to find, you’re lucky and only need to multiply using one fraction. However, this is not always the case. The number of fractions you’ll have to multiply in your setup depends on what conversion factors are available to you.
Here’s what I mean:
Suppose you want to know how many feet are in 4.6 miles.
In one situation you are given the following conversion factor(s):1 yard = 3 feet, 1 mile = 1760 yards
Which conversion factor would you start with? The one that has miles! How should the fraction be written? With miles in the denominator!
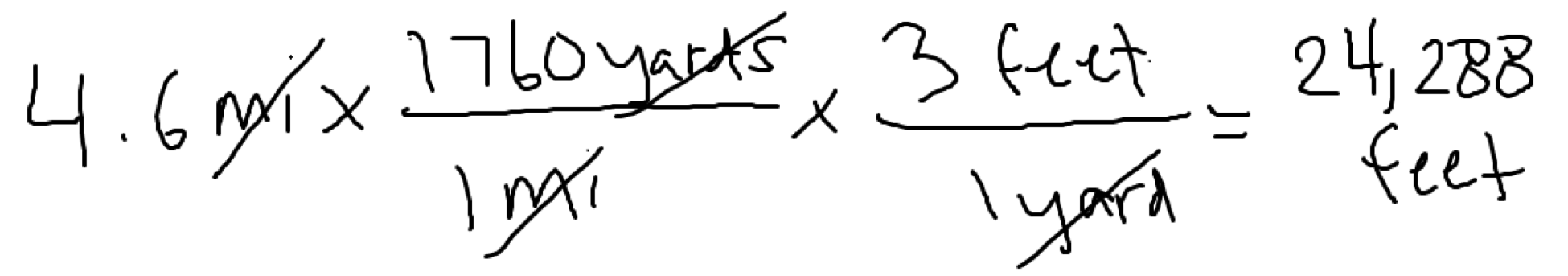
In another situation, you are given the following conversion factor(s):
1 mile = 5280 feet
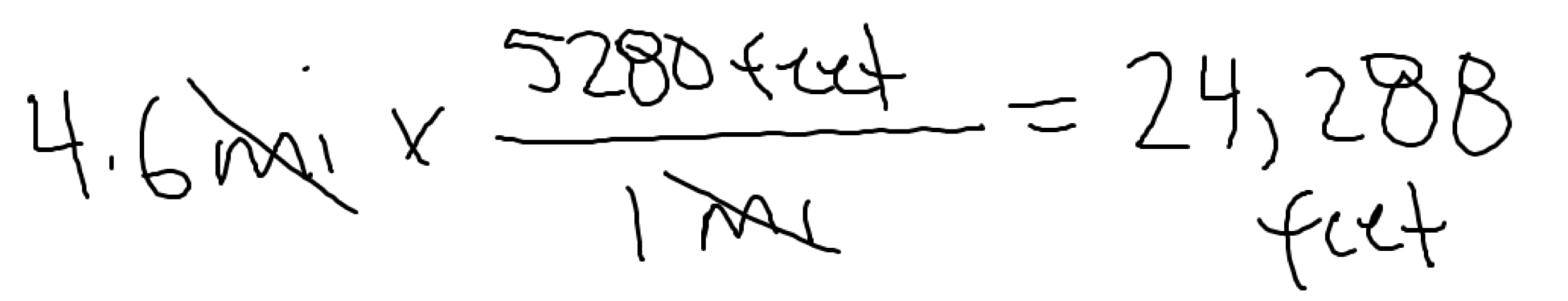
Both setups got us to the same answer but provided different conversion factors to use. One required us to use two conversion factors/fractions because no conversion factor was given that directly linked the units we started with to the units we wanted.
Conversions can get quite involved and require us to use three, four, five conversion factors/fractions. This doesn’t matter because you are simply multiplying by 1 repeatedly. Many general chemistry calculations can be used with the factor-label method alone.
To summarize, conversions that only require one step/conversion factor tend to be easy but for those that require multiple steps, the factor-label method allows you to remain clear and organized. The factor-label method also allows for you to always know where to at least start in a conversion. Remember, cancel out the unit you started with and go from there. Knowing where to start will give you the confidence and clarity to see where to go next. Lastly, it makes checking your work easy.

Comments