Last time on our physics tutoring blog, we conducted an experiment to investigate the influence of the moment of inertia on rolling motion. We started with two objects that had the same shape, but very different size and mass. Starting from rest, we then set them both rolling down a ramp, to see which one would reach the bottom first. The objects had different values for the moment of inertia, but nonetheless reached the finish line at the same time. So, we resolved to try a second experiment, repeating the first experiment but with two objects that have different geometries. Again, to keep it simple, we’ll stay focused on objects that have a circular cross-section, and that are easily found lying around the house. This time, we’ll pit the marble against a roll of masking tape. The roll of tape is larger and heavier than the marble, but from the analysis of our previous experiment we might expect the mass and size not to influence the outcome. Let’s see what happens:
And they’re off! Here is the view from the starting line.
And here is a close-up of the finish line.
We have a winner! The marble beat the tape by a clear margin. So, the geometry of the rolling objects is definitely a deciding factor in this race. Let’s take a look at the math, and compare with the previous experiment. For the roll of tape, we can approximate the shape to be a ring, which has a moment of inertia of I = MR2 when rotated about its center. Using the subscript m to denote the marble and the subscript t to denote the roll of tape, we can set up the energy balance equations in the same way as we did before:
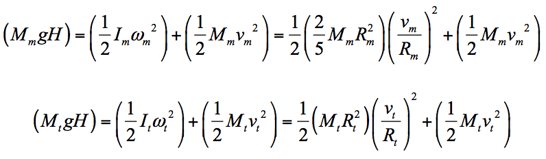
Here is that table of variables again, for clarity:
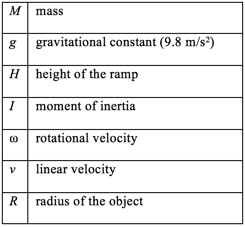
As before, the mass and radius of each object cancels out of the equations, and we are left with:
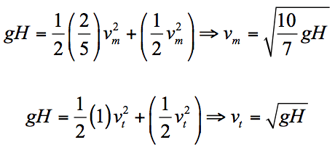
The velocity of the marble at the bottom of the ramp is greater than that of the roll of tape, which explains why we observe the marble crossing the finish line first. Comparing these two equations, we can see that the only difference comes from the rotational kinetic energy term – the first term on the right-hand side – where the marble has a factor of 2/5, the roll of tape has a factor of one. This factor is due to the moment of inertia! Without going too deeply into the mathematical details, remember that many common shapes have a moment of inertia with the form (inertia) = (some number) × (mass) × (radius)2. The number out front comes from a volume integral over the distribution of mass, which is clearly different for a ring and for a sphere.
So now we have an example of a real-world consequence of that pre-factor: in the case of our races, a certain portion of the energy each object starts with is converted into rotational motion, and the rest is converted into forward motion toward the finish line. The pre-factor in the moment of inertia then determines the balance between rotational motion and linear motion. For the roll of tape more of the initial energy is converted into rotation than into motion down the track, allowing the marble to come out ahead. The reason the marble and the pool ball were tied in the first experiment was that they have the same shape, and therefore the same pre-factor in the inertia. So what should happen if you match up the pool ball against the roll of tape? You can try this yourself, but it seems clear by this point that any solid sphere will beat any ring down the ramp. What about a cylinder versus a sphere? Well, the moment of inertia for a cylinder rotating about its axis is I = ½ MR2, so the pre-factor there would be ½, compared to 2/5 for a sphere. Based on our analysis, we would therefore expect the sphere to win. Cool, huh? Try it for yourself!

Comments