We already talked about Research Design and Execution, but there’s more to know about MCAT statistics! Here, we will be discussing topics that AMCAS wants you to know about Data-Based and Statistical Reasoning. Here’s what AMCAS wants you to know, and some tips to help you learn it! Use this post as an outline to guide your studying, and then come back to it later to clarify anything that might still confuse you, and make sure you haven’t missed anything important!
Data Based and Statistical Reasoning
(the text in bold is taken directly from the AAMC website!)
Using, analyzing, and interpreting data in figures, graphs, and tables
- Start by looking at the titles of the figure, graph or table. This will tell you what you’re looking for.
- Then look at the labels or axes. See if you can identify trends or patterns.
- Write a one-sentence summary of the relationship between the variables and add it to your passage map.
- If you don’t have a clue what’s going on in the figure or graph, take note of the variables it presents- keep the relationship between these variables in mind as you continue to read. Maybe you will get more explanation from the passage!
Evaluating whether representations make sense for particular scientific observations and data
- Distilled down, these are “common sense” questions. The table and these two figures all represent the same data:
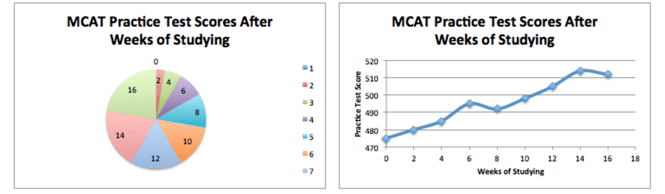

- Which makes more sense to represent the data? The pie chart doesn’t make much sense- each slice represents the proportion of the sum total of scores from all 8 tests. So you can see that the score in week 16 is higher than in week 8, but you don’t know what the score is! The line graph is a much better representation of the data.
Using measures of central tendency (mean, median, and mode) and measures of dispersion (range, inter-quartile range, and standard deviation) to describe data
- Mean: the average (495.1)
- Median: the “middle” number if you listed all the practice scores from lowest to highest (495)
- Mode: most frequent data point (the score you received most frequently-- in this MCAT score data set, there is no mode)
- Range: the minimum and maximum
- Interquartile Range: just like the median is the middle number, the interquartile range splits your data up into quarters. If your middle number is the median, then quartiles 1 and 3 (Q1 and Q3) are like the median of the data below and above the median (Q1 = 485, Q3 = 505)
- Standard Deviation: the “spread” of the data; on average, how far away from the true mean are the individual data points? A small standard deviation means that your scores were very similar to each other, while a large one means that you had a pretty widely variable performance on your practice tests. The standard deviation for these test scores is: 13.66)
Reasoning about random and systematic error
- Random error: error that is unpredictable and from unknown sources; this error makes you less sure about your results but probably won’t skew them one way or the other
- Systematic error: error that comes from a problem with how you’re doing the measuring- maybe you’re misapplying the scoring formula in whatever practice book you’re using
Reasoning about statistical significance and uncertainty (e.g., interpreting statistical significance levels, interpreting a confidence interval)
- Statistical significance level: your “alpha.” If your alpha is 0.05, or your results are “significant at 0.05” that means that there is a 5% chance that your result was due to chance alone. For most sociological and biomedical research, 0.05 is the gold standard.
- Confidence interval: usually we use 95% confidence interval. If you wanted to know the average height of every adult man in Manhattan, you would have to measure every single man in that population to get the TRUE average. However, we don’t have the time or resources to do this, so we will take a random sample of men in Manhattan and measure their heights. We will get an average height of our sample. The 95% confidence interval is constructed around this sample mean, and gives a range above and below the average height in our sample. We can assume that if we picked another random sample of men in Manhattan and measured their heights, 95% of the time the sample mean for this second population would fall somewhere within the 95% confidence interval we constructed for our first population. Furthermore, we are 95% certain that the TRUE average height of ALL the men in Manhattan would also fall within this range.
Using data to explain relationships between variables or make predictions
- Identify relationships: if variable A increases, what does variable B do?
Using data to answer research questions and draw conclusions
- Does our data make a good case for our conclusion? Usually, if something is “significant at 0.05”, then we are confident that our data show that the effect we are observing is NOT just due to chance, and therefore due to our intervention.
Identifying conclusions that are supported by research results and determining the implications of results for real-world situations
Even if you’ve never taken a statistics class, you probably have a much better grasp on this material than you think. Remember, you’ve been hearing about statistics your whole life- on TV commercials, on the news, on cereal boxes. While it may seem intimidating at first, try to break everything down into “common English” like the examples in this post.

Comments