
Complicated algebra is the last thing many students want to deal with on a high-stakes test like the SAT or ACT. Yet it seems like there is no way around it, with the alphabet soup of variables scattered throughout the exam. Thankfully, there is a strategy for those problems where your algebraic manipulations are leading nowhere. It’s called plugging in numbers.
Let’s take this problem, for example.
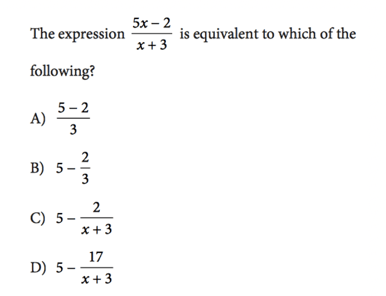
At first glance, we might have no idea how to get from the given expression to one of the answer choices. We’d definitely have to do some kind of algebraic gymnastics, which we want to avoid for many reasons! First, we may just not know how to get where we need to go. Second, algebra isn’t that easy, and we’re liable to make mistakes along the way. But what if there were a way to solve the problem using just simple arithmetic? Thankfully, there is! That’s where plugging in numbers comes in.
For the plugging in numbers strategy, our first step is to identify the variable. Here, the variable would be x, of course. In other cases, where there is more than one variable, you would want to choose the one that appears the least times and plug in for it first to solve for the other variables. But back to this problem, we always want to start by plugging in the smallest number possible, either 0 or 1. This will really save us time on our later calculations and also reduce the chance we make a mistake. Note, these numbers may not work for all problems – you may end up dividing by 0 sometimes, in which case you need to choose a different number.
After we’ve identified the variable and chosen a number to plug in, the next step is to plug that number in for all the places it occurs in the question. So here we plug in x = 0 and find that the expression becomes 5(0) – 2 / (0 + 3), which is equal to -2/3. Since the question is asking for what this expression equals, this is the goal number we’re looking for in the answer choices. So we’re going to make a big circle around that goal number, 2/3.
The next step, after we’ve gotten our goal number, is to plug into all of the answer choices. Here, since A and B do not have any x’s, we only need to plug into choices C and D. For C, that gives us 5 – 2/(0+3) which equals 4 1/3. For D, that gives us 5 – 17/(0+3) which equals -2/3. Finally, since A and B are not simplified, we need to simplify them which gives us 1 for A and 4 1/3 for B. Now the final step is to cross out all the answer choices that do NOT equal our goal number, so we cross out all choices besides D. That leaves D as our answer. See how much easier that was than figuring out the complicated algebra?
Note, we do not just stop once we get a choice that equals the goal number because sometimes more than one answer choice will end up equaling the goal number. In that case, we would cross out all choices that do not equal the number, since those must be wrong. We would then plug in another number for the variable into the question, find a new goal number, and then plug into the remaining answer choices. If needed, we would repeat the process until only a single answer choice remained.
Now that you’ve learned this technique, you’re well on your way to solving those difficult algebra problems on the math section of the SAT and ACT! Just keep practicing to get the strategy down pat so you’ll have no problem doing it smoothly under pressure.

Comments