Trigonometry should be simple—you’re just using the given information to solve for only one answer, right? Well, with the Law of Sines, sometimes there is more than one right answer. This situation is also known as the Ambiguous Case. Before we dive into the Ambiguous Case, let’s review the Law of Sines and Congruence.
The Law of Sines
The Law of Sines relates all angles and sides of a triangle in the following way, in which the lowercase letters indicate the side directly across from the capitalized angle:
A Refresher: Showing Congruence
By now, you know that you can use a combination of sides and angles to prove congruence between two triangles. For example, if you know the length of all sides, you can find all of the angles of that triangle. The side-side-side (SSS) example is one way to prove congruence. Others include: angle-side, angle (ASA), side-angle-side (SAS), and angle-angle-side (AAS). You may have noticed that with side-side-angle (SSA), that is not the case, which leaves the triangle unclear, or ambiguous.
Here’s a tip to help you remember which set of conditions results in the Ambiguous Case: what’s SSA spelled backwards? (This is sometimes referred to as the Donkey Rule, but you didn’t hear this from us!)
The Ambiguous Case
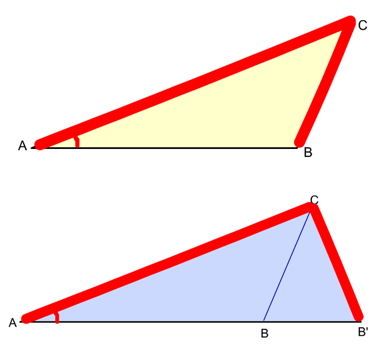Don’t believe us? Let’s draw it out!
In the first triangle, we are given side BC, side AC, and angle A, creating an SSA scenario. Now, what if we take B and sweep it outwards to B’? The second triangle shows the result. Our givens (BC, AC, and angle A) remain unchanged, but we have a second triangle.
Note: This won’t always be the case. In the Ambiguous Case, sometimes two triangles will be possible, sometimes one, and sometimes (but not often) none. It is our job to find out how many possible triangles are created by the set of conditions we are given.
So, our first task is to find out if one triangle exists. If it does, we will move on to see if there is a second. Want to see how it’s done? Read on!
Example 1: No Triangles Exist
Consider a case where angle A is 65 degrees, side a (or BC) is 18 units long, and side b (or AC) is 22 units long. How many possible triangles exist?
We want to use our three unknowns, so we will set up the Law of Sines using sides a and b and angle A, solving for angle B.
Since sin(B) is greater than 1, it is undefined. Therefore, no triangles exist for this scenario.
Example 2 - One Triangle Exists
Now, consider a case where angle A is 58 degrees, side a is 25 units long, and side b is 22 units long. How many possible triangles exist?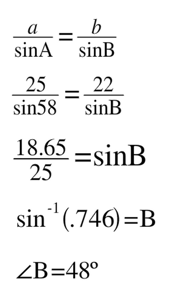
Following the same method as we used in Example 1, we’ll solve for angle B. Using this method, we find that the one triangle exists with an angle B equal to 48 degrees. Does another exist?
To prove that another triangle exists, we must determine if another possible angle B exists that makes the triangle possible. Notice the isosceles triangle created by the Ambiguous Case above. So, B’ and B are supplementary angles, or 180 = B’+B. This means the second angle B is 132 degrees.
Since we know all angles in the triangle must add to 180 degrees, a second triangle is not possible because angles A and B alone exceed 180 degrees.
Example 3 - Two Triangles Exist
If a second triangle was possible, angles A and B would sum to a number smaller than 180 degrees. Let’s repeat the example above, but this time, we will shrink side A to 20 units.
Comments