Overlapping what?
Overlapping sets are, by far, one of the most complicated topics on the GMAT. Any good GMAT coaching regimen should focus on demystifying this topic. But if you put in a little bit of elbow grease and apply a formulaic approach, these seemingly overwhelming questions can score you big points. As a private GMAT tutor in Boston, I’ve worked with students and developed some effective strategies that I’ll share in this post.
There are two types of overlapping sets.
Here’s the big picture definition: overlapping set questions assign things a particular trait. Maybe you are looking at a class of high school students who either take Spanish, French or both. Maybe you are looking at a survey of men and women who either voted for or against a bill. We can define the two types as single- or double-trait questions. With single-trait questions, everyone is assigned one or more attributes within a given trait. With double-trait questions, everyone is assigned two attributes, one for each of two traits.
The Single-Trait Question
Tackling the single-trait question is easy with a Venn Diagram. Consider the following question:With lots of numbers here, the crucial step is organizing information into a Venn Diagram.
TOTAL #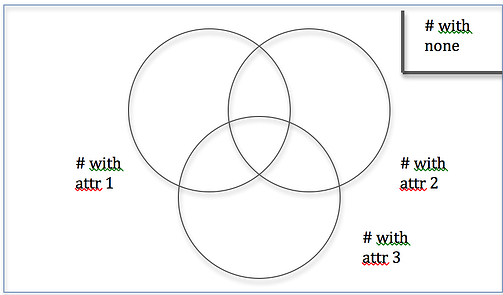
The diagram above presents a standard framework for single-trait overlapping sets. Begin by filling in all of the information that you know, and then assign variables to the information you do not know, and solve. For the language example, we have the following:
100 students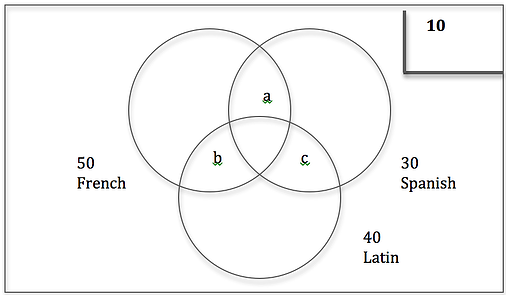
So now that everything is filled in, we can start to solve. Given that there are 100 students in the class and 10 do not take a language, we have 90 students who do. However, if we add 50 + 30 + 40, we get 120 students. This is because we are double counting regions a, b, and c on the diagram. Therefore, we would have to subtract out a + b + c, which must be equal to 30 students. This means that 30 students take two languages.
To put this algebraically, French + Spanish + Latin – (a + b + c) = Total – None.
However, no need to memorize any algebra; instead, just draw the diagram and think through it logically.
The Double-Trait Question
Approaching the double-trait question is a little different. Here, each individual has two attributes, and the objective is often to find out what percentage of individuals with one attribute also possess the other. This is handled very nicely with a table. Consider this example:
Of the 10,000 residents of City X, 40% are women and 60% voted in favor of a particular bill. If 30% of the men in City X voted against the bill, how many women voted in favor of the bill?
Again, lots of numbers here, so let’s start a table with the information we know:
|
|
Men |
Women |
Total |
|
Vote yes |
|
??? |
6,000 |
|
Vote no |
30% |
|
|
|
Total |
M |
4,000 |
10,000 |
While we were given this information directly, we can also infer some more information. For example, the number of men must be 6,000 (since 40% of 10,000 are women) and therefore the number of men that voted no is 1,800 (30% of men voted against the bill). Also, the total who voted no is 4,000 (since 60% of 10,000 voted yes). Filling in this information, we are left with:
|
|
Men |
Women |
Total |
|
Vote yes |
|
??? |
6,000 |
|
Vote no |
1,800 |
|
4,000 |
|
Total |
6,000 |
4,000 |
10,000 |
Now that we have established this, the last step is to fill in the remaining three squares by subtracting from totals:
|
|
Men |
Women |
Total |
|
Vote yes |
4,200 |
1,800 |
6,000 |
|
Vote no |
1,800 |
2,200 |
4,000 |
|
Total |
6,000 |
4,000 |
10,000 |
The answer is 1,800. Do you see how making a table allows you to organize information, and systematically determine the answer to a question? From my experience as a private GMAT tutor in Boston, I’ll reemphasize that this is one of the most crucial skill for students to develop.
Summary
Remember that systematic thinking is key to solving these problems. Overlapping set questions are very common but present a complex set of difficulties. Like many questions on the GMAT, the most important part of solving the question is to fully understand and rephrase it. To reiterate the key steps:
- Identify how many decision variables there are. This will inform the framework that you should use to populate given and required information.
- Draw a diagram (Venn or table).
- Fill in obvious known information and highlight what is being asked, being sure to use totals to your advantage.
- Iterate this process and solve for the unknown piece of data.
As long as you keep this systematic approach in mind and avoid common pitfalls (e.g. confusing totals with individual pieces of data, mixing up single- and double-decision variables), you should be able to effectively demystify questions of this type. Here are some additional blog posts written by fellow private GMAT tutors that you may find useful: on back solving, changing your approach, and the process of elimination. If you’d like additional support, we’re happy to offer in-person GMAT coaching in Boston and New York, and online GMAT coaching anywhere around the world. Feel free to get in touch!

Comments