 As an overarching theme, I’ve tried to stress that there is more to studying physics than slogging through the math. Instead of treating a problem as a series of dry mathematical manipulations, a sequence of numbers that, when punched into the calculator in the correct order, will yield your answer, we should always try to think about the physical intuition that underlies the problem.
As an overarching theme, I’ve tried to stress that there is more to studying physics than slogging through the math. Instead of treating a problem as a series of dry mathematical manipulations, a sequence of numbers that, when punched into the calculator in the correct order, will yield your answer, we should always try to think about the physical intuition that underlies the problem.
We’ve discussed how staying abstract, holding off on plugging in numbers until the end of a problem, can speed up your problem solving. We’ve also talked about how considering the relevant units of a problem, seeing the quantities you’re given as physical lengths, and masses, and velocities instead of as numbers on a page, can help you intuit the answer to a problem without getting bogged down in the math. In this post, let’s put these two strategies together.
“Does my answer behave the way that it should?”
So you’ve done the algebra to find an expression for your answer, and you’re about to plug in numbers. How do you know, though, that your expression is correct?
As we discussed in a previous post, the first question you should always ask is, “Is my answer the right kind of quantity?” That is, do the units work out? Were you asked to find a time and is your answer in terms of seconds?
The second question you might want to ask is, “Does my answer behave the way it should?” This is a poorly defined question, and intentionally so. The trick, as you’re staring at your answer trying to decide whether or not it makes sense, is knowing what questions to ask yourself. Let’s go over a few common possibilities.
“Is it missing anything? If so, does that make sense?”
The problem gives you a set of quantities, so it stands to reason that most or all of them should find their way into your answer. Problems will occasionally throw you red herring numbers that you never need to use, but quantities will more often drop out of your equations for more physically interesting reasons.
Let’s say that you are asked to find the orbital period of a satellite of mass m, which is orbiting Earth (mass M) at a height of 1,000 km. If we assume that the pull of the satellite does not cause the Earth to accelerate (M is much, much larger than m), then we should find
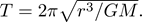
Notice anything missing? Does it make sense that the period of a satellite’s orbit should be independent of its mass? Since the centripetal force needed to keep the satellite in orbit and the force of gravity are both proportional to the satellite’s mass, m cancels out. This is why an astronaut can float next to the space station and not drift away as they circle the earth.
“Does the sign make sense?”
This question usually helps catch mistakes arising from mixing sign conventions. If you throw a ball upward and it takes a negative amount of time to reach the top of its arc (zero vertical velocity), does this make sense? If you defined the initial velocity to be positive, should the acceleration due to gravity be positive or negative?
“Does it work in sensible limits?”
If you set various quantities in your answer to limiting values, usually zero and infinity (or “x much larger than y” and “x much smaller than y”), does your answer still make sense? This approach is powerful because these limiting cases are often very easy to imagine physically.
In a canonical example, a bullet of mass m is fired at velocity v into a block of mass M, and we are asked to find the combined velocity V at which they fly off together. How fast are they moving? Using conservation of momentum, we should find
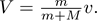
What limits should we try? What if m and M are equal? In that case, V = v/2. This seems about right, but we might not be absolutely sure. At least V is less than v, which we can intuitively know is correct.
Let’s try setting m to zero, or saying that M is much larger than m. In this case, V is zero. Does that make sense? If you throw a snowball at an iceberg, does the iceberg move?
Alternatively, let’s try setting M to zero, or saying that M is much smaller than m. In this case, V = v. If a Boeing 747 flies through a storm and a (stationary) raindrop sticks to the windshield, does the plane slow down appreciably?
I find that this approach works particularly well when dealing with angles. Say a block is sliding down a ramp that is inclined at a certain angle. Is the normal force proportional to the sine or the cosine of the angle? Imagine setting the angle to zero. Now you’re just dealing with a block sitting on a flat surface. Is the normal force now zero, or is it now equal to the full weight of the block? Given this result, must the normal force be proportional to sin(0) or cos(0)?
Imagine that you were asked to the find the time it takes for the block to slide to the end of the ramp. Does it make sense that the block would take an infinite amount of time to slide to the end of a flat ramp? If you find that it takes zero time, what might have gone wrong in your calculations? What if you found that it takes the block a finite time to slide to the end of a flat ramp?
The great thing about physics is that you’re dealing with real, visible, tangible objects. You should use this to your advantage! You intuitively know, more or less, what happens to objects in the real world, be they cannonballs, or cars, or the sirens of passing ambulances. Physics problems are often only asking you to express quantitatively what you already know to be true, so use the above questions and your own physical intuition to help you do physics with confidence!
Comments