Electron configurations: a must know hack

Imagine this...you’re taking your general chemistry midterm and you’ve decided to shuffle through the exam and complete all the hard things first. You’ve totally underestimated how much time those problems were going to take you and now you have three minutes left to write the electron configuration of 10 elements. Untimed, this would be easy to do. It’s systematic and straightforward but still requires a decent amount of thought based on how you were taught to do it. Your palms get sweaty. These are supposed to be easy points and there’s a possibility that you won’t complete it. If you do complete it, there’s a possibility that you’ll get them wrong because you were rushed. Your throat is getting tight at this point. You’re trying to recall if you were confident about the other questions you have already done, wondering if you can afford to lose these easy points in front of you. Your teacher announces that there are two more minutes before he starts collecting exams.

What if I told you that there was a faster and flawless way to determine electron configurations? 

What are electron configurations and why do we care?

As you know, protons and neutrons are found in an atom’s nucleus. The nucleus is at the center of an atom; therefore, protons and neutrons are easy to locate.

Since electrons are not found in the nucleus, they can literally be anywhere because the nucleus only takes up a small space of what seems to be a huge amount of ground to cover. Thus, finding an electron can be quite difficult. It’s kind of like looking for a needle in a haystack. Why do we care about finding electrons? Because electrons are the MVP of chemistry. In a nutshell, they’re the reason atoms are able to interact with other atoms.

Electrons can be found in orbitals, a region in space around the nucleus where there is a high (90 %) probability of finding an electron. Orbitals are not an exact place but rather an area that includes that exact place. 

An electron shell or energy level is a collection of orbitals within the same probable distance from the nucleus. Each shell has one or more subshells within it. Each subshell has one or more orbitals within it. Each orbital holds two electrons.

The periodic table consists of elements, all of which multi-electron atoms (except hydrogen of course). Electron configuration tells us how these electrons are distributed among the various atomic orbitals. They show up on general chemistry exams without fail. 

The conventional way to determine electron configuration

As previously mentioned, electron configuration is a particular distribution of electrons among available orbitals. It lists the orbital symbols sequentially with a superscript indicating the number of electrons occupying that orbital. In a neutral element, the number of protons is equal to the number electrons it has. The more electrons an element has, the more orbitals it will have to fill.

There are a few rules that must be followed when writing electron configurations. They will not be covered here. My point in mentioning them is to highlight the fact there is a specific order to how we fill up the orbitals:

This is a memory aid that everyone that has ever taken general chemistry has seen. Follow the diagonals sequential, from tail to head. Remember that s gets two electrons, p gets six electrons, d gets 10 electrons, and f gets 14 electrons. But I’m not here to teach you how to use this conventional method. I’m here to tell you what’s wrong with it:

1. You have to remember this memory aid, diagonals and all.
2. You have to keep a tight tally of the electrons you’ve used so far so you don’t go over the number of electrons in the element you’re working on.
3. You have to remember how many electrons fit into each subshell (s, p, d, f).
4. It takes a lot of time, especially when the element has more than 20 electrons.

The better way to determine electron configurations: the block method

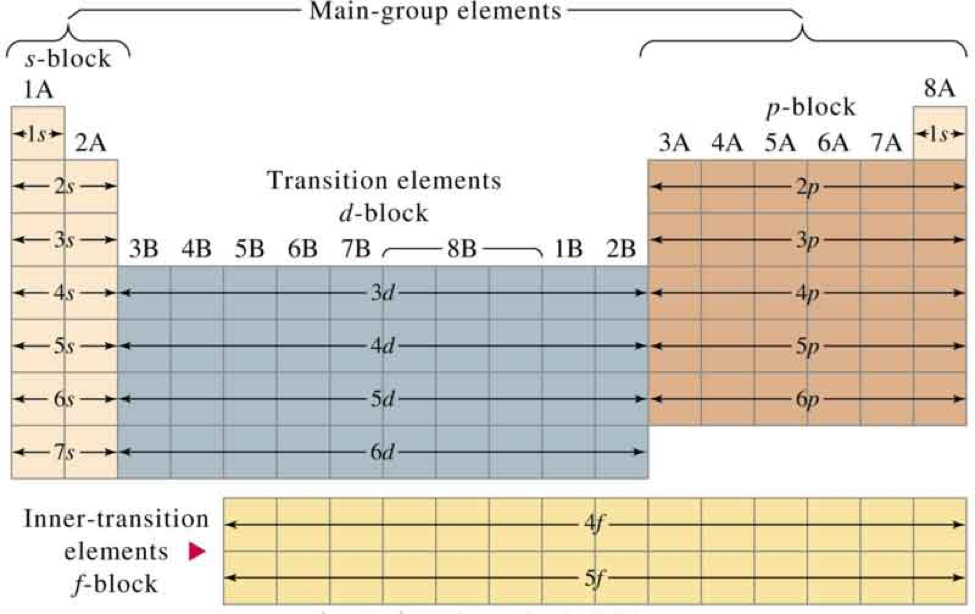
The picture above is the solution to all your electron configuration problems. This is a periodic table that has been labelled in blocks. Notice that, for the d block, the coefficient or number in front is always one less than the row it is in. For the f block, the coefficient is always two less than the row it is in. You’ll have to remember this. When it comes to general chemistry, there’s always going to be things that you just have to remember. Even hacks require some brain work. But besides labeling the clean periodic table when you receive it on test day like you see it above, that’s literally it. So, how do you use it?

Step 1: Label your period table in blocks.

Step 2: Identify the element of interest on the periodic table and circle it

Step 3: Locate hydrogen as your starting point

Step 4: Glide across each row, left to right and top to bottom, writing out the electron configuration until you get to your element.

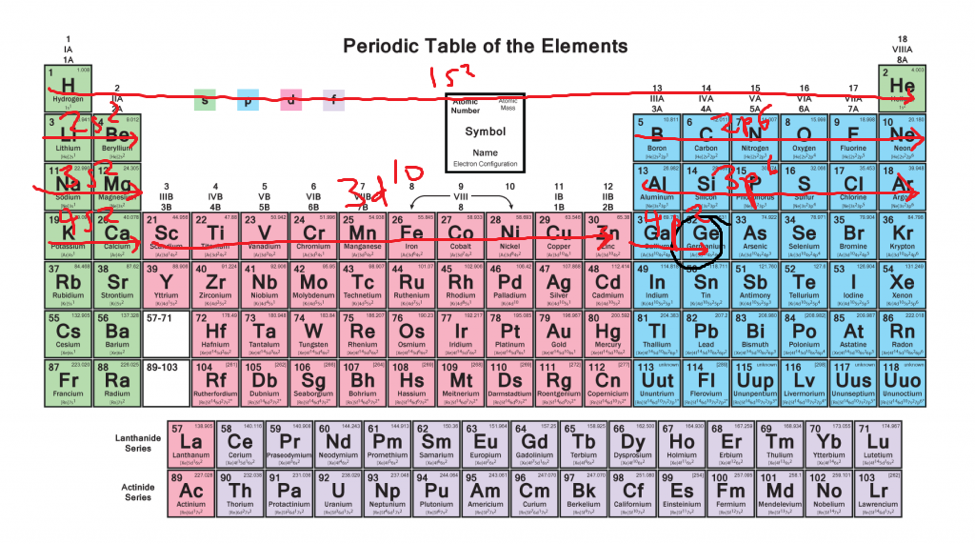
Ge: 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p²

• Do not move to the next row until you’ve completed the row above it.
• Count the number of elements you pass by for each block. That is your superscript.
• When the d block finally gets incorporated, remember that its coefficient is one less than the row that it is actually in. If you’ve labelled in advance, this will be obvious.

Step 5: Check your work by adding all the superscripts and seeing if it adds up to the total number of electrons in your element of interest. This is optional. 

2+2+6+2+6+2+10+2 = 32

Here’s a list of things that makes this a much better method:

1. You don’t have to remember how many electrons fit into each subshell (s, p, d, f).
2. You don’t have to remember that annoying memory aid, diagonals and all.
3. You don’t have to keep a tight tally of the electrons you’ve used so far so you don’t go over the number of electrons in the element you’re working on.
4. It takes much less time and elements with more than 20 electrons aren’t a drag.
   
   

Don’t believe this is flawless? If you’re not a believer, try the block method on a few elements and check your work with the conventional method.

Now back to that midterm of yours. Where were we? Oh yes, two minutes to do 10 electron configurations. You finish with only seconds to spare. Good thing you used the block method.