Gaining intuition for Taylor series

I’m writing this blog post because when I first came across Taylor series I found that a lot of my previous intuitions for mathematics were suddenly inadequate. It took time for me to build intuition not only for how these things work but why they are important. I hope this post will be illuminating for those just beginning to learn about Taylor series and also those who have some experience with them but haven’t quite wrapped their heads around them yet.

First, recall that a series is defined as a finite or infinite sum of terms. For example:

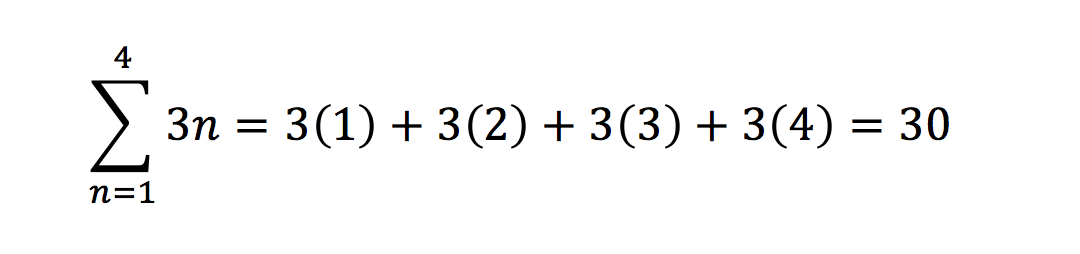
The above is a finite series. We can sum series to finite amounts or to infinite amounts:

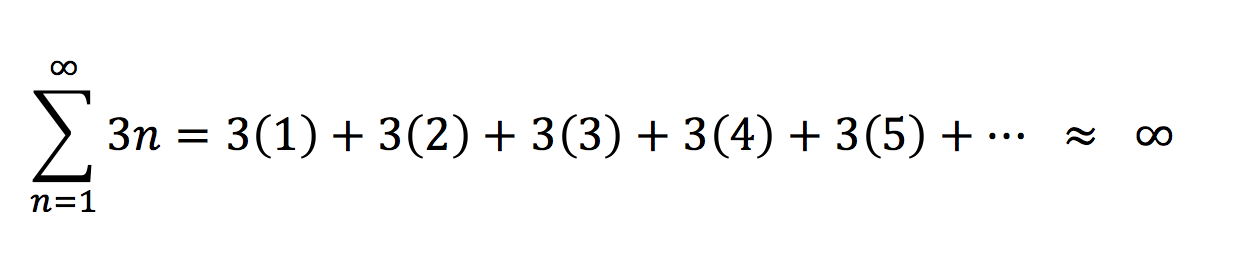
And, we say that these infinite series either converge to a specific finite number, or as in the case above, diverge towards infinity. Series don’t just represent numerical quantities, though. We can use them to conveniently represent certain kinds of polynomials. For example:

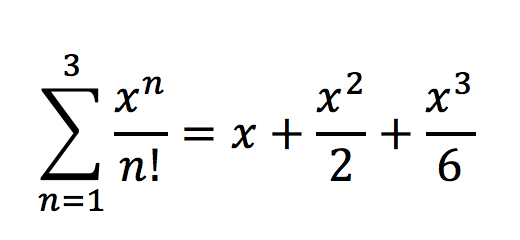
Mathematics – from high school math to graduate school math – is one of our most frequently requested subjects. Teaching math is notoriously difficult and we maintain a staff of mathematicians who are committed to the art of teaching. There is no course or standardized test that we do not have extensive experience teaching. We work with students who loathe math and students who love it, students who haven’t done math in a decade and students who work on mathematical problems every day. Many of our students work with tutors to address courses or exams – such as Geometry, Linear Algebra, Differential Equations – but we also work with students looking to explore more advanced or unconventional topics (like the mathematics of poker, or algrabraic topology, for example).

Check out some of our previous blog posts related to mathematics below!

An Application of Calculus: Finding Optimal Road Networks

What is Mathematical Induction (and how do I use it?)

An Insider's Tip to Prepping for the SAT Math Section: Plug in Numbers