An everyday limiting reactant problem
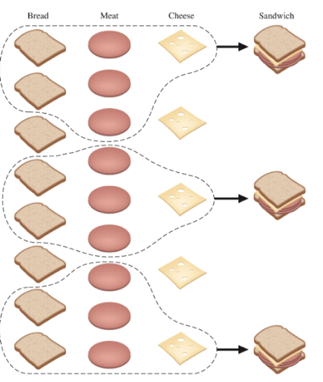
You’re expecting company and totally forgot to go grocery shopping. What on earth will you feed your guests? Sandwiches! You have some ingredients to whip up some sandwiches. So, let’s assume you are going to go through with making these sandwiches. You need 2 slices of bread, 3 slices of meat (can’t be stingy), and 1 slice of cheese for each sandwich. After raiding your refrigerator, you discover that you have 8 slices of bread, 9 slices of meat, and 5 slices of cheese. You worry that this won’t be enough. How many sandwiches can you make?
Oh, this is easy. 8 slices of bread, 2 slices per sandwich – 4 sandwiches! But wait. 9 slices of meat, 3 slices per sandwich – that would only make 3 sandwiches. But wait. 5 slices of cheese, 1 slice per sandwich – that would 5 sandwiches! Well once the slices of meat run out after sandwich number 3, you won’t be able to make any more sandwiches. And no, you’re not interested in making grilled cheeses. So, you can only make 3 sandwiches. The meat determined how many sandwiches you could make in completion. It made the least number of sandwiches. Thus, the meat is the limiting reactant!
Here's the math:
- Bread: 8 x (1 sandwich ÷ 2 slices) = 4 sandwiches
- Meat: 9 x (1 sandwich ÷ 3 slices) = 3 sandwiches
- Cheese: 5 x (1 sandwich ÷ 1 slice) = 5 sandwiches
What is a limiting reactant and why do they exist?
A limiting reactant (or limiting reagent) is a reactant that is entirely consumed when the reaction goes to completion. It ultimately determines how much product can be obtained. The excess reactant (or excess reactant) is the reactant that is not entirely consumed when the reaction goes to completion. Some of it will remain after the reaction is complete. In the scenario above, 3 sandwiches were made at completion of the sandwich-making process. No meat was leftover, making meat the limiting reactant. 2 slices of bread and 2 slices of cheese were leftover, making bread and cheese excess reactants.
In the scenario above, it was a matter of chance that there were reactants in excess. I’m sure if you could have it your way, you’d have acquired the correct number of each sandwich component so that there would be no leftovers. In chemistry, excess reactants are deliberate.
What sense does this make? You wouldn’t be able to make any more product than what the limiting reactant has determined. So why not just provide the “equal” amounts of all the reactants so that none is wasted? Especially if you know just how much product you want to make? Well, chemists hardly ever carry out reactions with “equal”, or stoichiometric, amounts of reactants. One is always in excess because the more reactant added, the faster the reaction will occur. Principles of kinetics in its purest form, beyond the scope of this post. Chemists want to get their products as quickly as possible and an excess reactant accomplishes this.
The approach to limiting reactant problems
These problems are going to provide you with starting amounts of reactants and ask you how much product can be made from them. Just like the sandwich dilemma. But one thing is missing that is crucial. Just like we were told how much of each sandwich component were found in one sandwich – the sandwich formula, we need to be told how much of each reactant will be found in a certain amount of product. This is where balanced chemical equations come in.
Consider the following balanced chemical equation:
2A + 4B --> 3C
The coefficients show:
- Relative numbers of molecules of reactants and products.
- Relative number of moles of reactants and products, which can be converted to mass.
Moles are your best friend and should always be used to interpret balanced chemical equations because they are easier to work with since molecules are too small and because they can be converted easily to mass which is how most express “how much”.
An interpretation of the balanced chemical equation above would be: to make 3 moles of C, you need 2 moles of A and 4 moles of B. If you wanted to know how to make 1 mole of C, divide the whole equation by 3. To make 1 mole of C, you need 2/3 moles of A and 4/3 moles of B. This is obviously a mouth full and hence why we use whole numbers to balance equations.
Now, we have all the information we need to determine how much product made.
- Determine the limiting reactant by considering each reactant as independent and determining how many MOLES of product would be made from its starting amount. Just like you did for your sandwiches, do this for all the reactants.
If the starting amount of reactant is provided in grams, use dimensional analysis and follow the schematic below:
*Substance A is the reactant and substance B is the product of interest*
If the starting amount of reactant is provided in moles, it’s much simpler:
- Whichever reactant created the smallest number of product in moles is your limiting reactant. You’ll run out of it first and won’t be able to make any more product.
- Check the question to see how they want you to express the “how much” of product.
If they want in moles, you’ve already found it. It’s nothing more than the smallest of the moles of product you calculated from the independent reactants.
If they want in grams, convert those moles to grams:

Putting these steps into practice
Zinc metal reacts with hydrochloric acid by the following reaction:

If 0.30 mol Zn is added to hydrochloric acid solution containing 0.52 mol HCl, how many moles of H2 are produced?
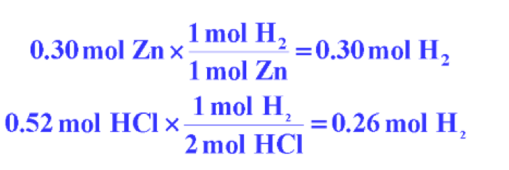
- HCl made the smallest number of H2 in moles and is thus the limiting reactant.
- The amount of H2 produced must be 0.26 mol.

Comments