In business, finding the right price for your product is crucial. Price it too high, and few people will buy; price too low and the business leaves money on the table. But how do you determine the right price? We will explore this question with a simplified example, looking at Umbrella Corp (UCorp). Note that in this simplified case, UCorp is a monopolist and cannot charge different prices to different customers (i.e. is unable price discriminate).
Step 1: Estimate the demand curve
The first step is to estimate the demand curve of UCorp’s customers. In real-world settings, companies can use several tools to estimate the demand curve for a product such as customer surveys, market experiments, regression analysis and others. In our example, to estimate the demand for umbrellas, Ucorp asked a class of 80 students to raise hands if they are willing to buy an umbrella at various price points on a rainy day.
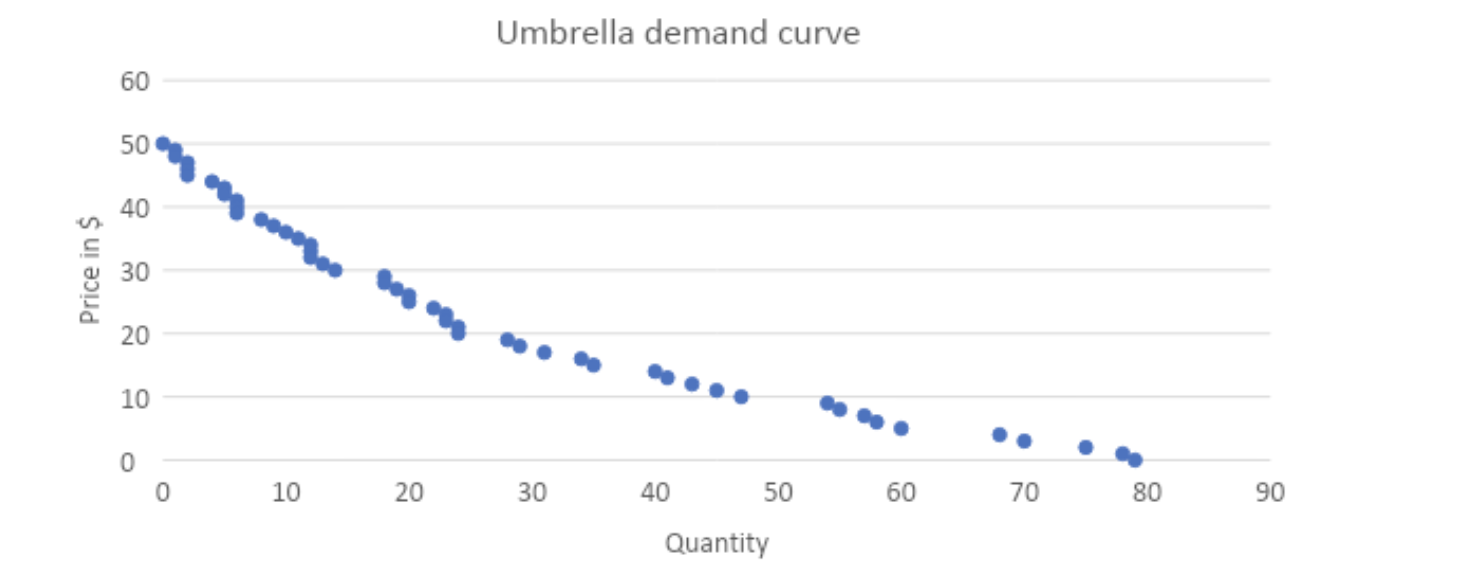
The outcome of this experiment is the demand curve depicted in Graph 1: no student raised a hand at a price of $50 per umbrella and all 80 students would have taken an umbrella for free.
Graph 1: Umbrella demand on a rainy day at various prices
Step 2: Graph the revenue curve and determine revenue maximizing quantity/price
Assuming the student population is representative of UCorp’s target customer, the company can now estimate its revenue at various price/quantity combinations, see graph 2. To do that with a dataset quantity sold at each price with the price to find the highest revenue.
Graph 2: UCorp’s revenue at various quantities sold

Note that UCorp achieves its maximum revenue ($600) selling 40 umbrellas at a price of $15 each.
Decreasing the price by $1 would lead to falling revenue, as the loss in revenue from existing customers is greater than the revenue from new customers (the 40 existing customers would each pay $1 less, whereas only one new customer would be paying an extra $14, leading to a net revenue loss of $26).
Likewise, increasing the price by $1 would lead to a revenue of $560 or $40 less than at the revenue maximizing price point of $15. (35 customers would each pay an additional $1, however, 5 customers would be lost that had paid $15 per umbrella before, resulting in a net revenue loss of $40).
Step 3: Find profit maximizing quantity/price
If the goal was to maximize revenue we would be done, but the goal is to maximize profit, so we have to introduce costs. Let’s assume that UCorp has some fixed costs (F) to manufacture umbrellas and that variable costs (labor, capital and material) per umbrella are constant (c).
Cost equation: C=F+c×q Note: In this case F = 100, c = 5;
Profit equation: P=p*q-F+c×q=p-c*q-F
Intuitively, we know that UCorp should produce umbrellas as long as the revenue from each umbrella is greater or equal to its variable cost (p=c), or in Econ language, Ucorp’s optimal output is determined at a quantity/price combination where marginal revenue is equal to marginal cost (MR =MC).
In this case marginal revenue is equal to the price (the revenue for each additional unit sold is the price of one umbrella) and marginal cost is the variable cost (the cost of each additional umbrella produced is marginal cost), so we can substitute MR with p and MC with c.
Graph 3: UCorp’s profit at various quantities
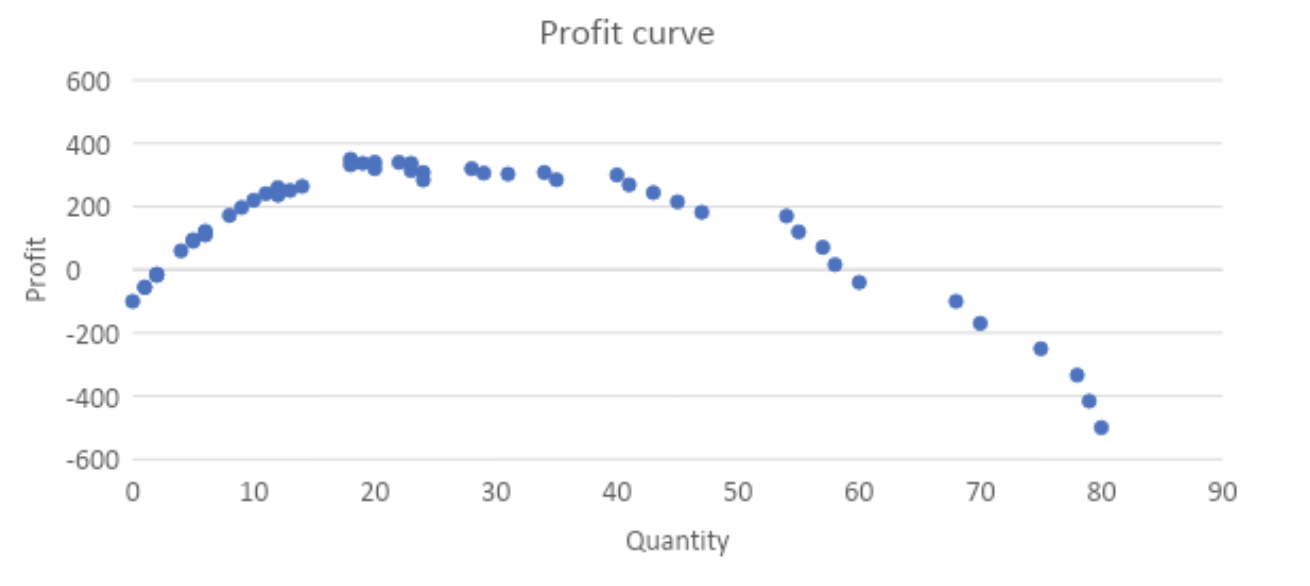
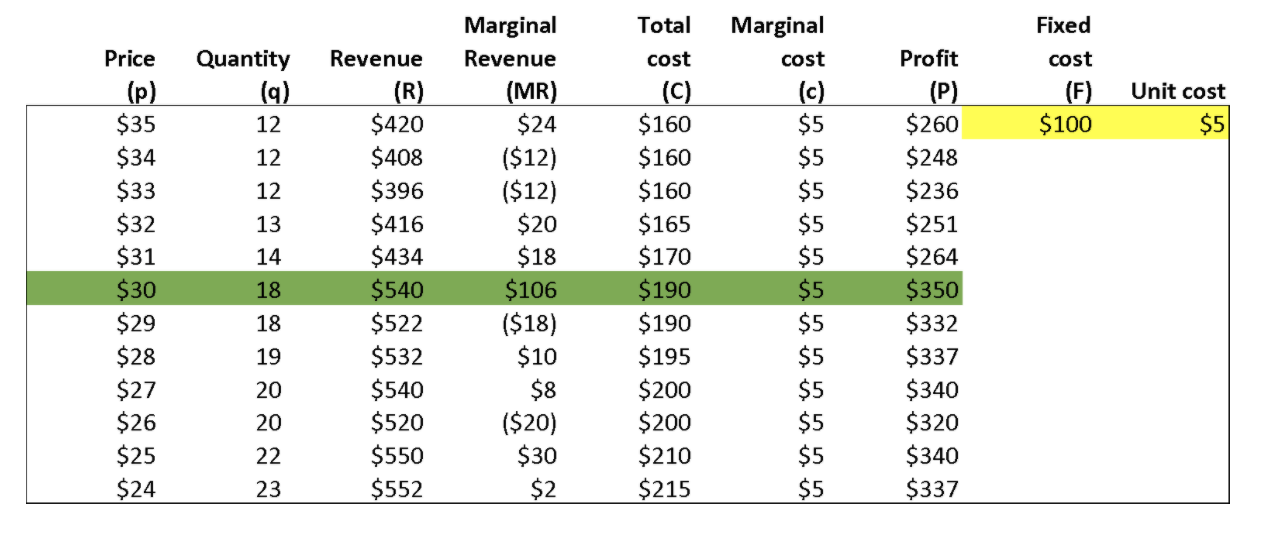
In this case with F=100 and c=5, UCorp would choose to only sell 18 umbrellas at a price of $30 per umbrella to generate revenue of $540. Even though this leaves revenue lower than the maximum of $600, UCorp generates higher profit ($350 vs. $300) as it saves 22 x 5$ = $110 in costs.
In summary, to determine the optimal price to charge, a business needs to understand its customers, in particular their demand behavior, and its own cost structure.
Appendix: Data table excerpt
Curious about the intersection of business and economics? Looking for support for a course? Our team of MBAs, PhDs in Economics, and working professionals are here to help!


Comments