How to use the ideal gas law

While you might not think about it very often, gases are everywhere around us, from the air you breathe to the natural gas you might use to heat your home. To use gases safely and effectively, chemists use the ideal gas law to understand how much gas is in containers and pipes.

The ideal gas law is an equation that relates the pressure (P), volume (V), temperature (T), and amount of gas present (n) in a container. In its complete form, it looks like:

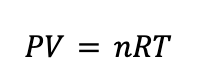The R in the ideal gas law is an important constant called the ideal gas constant, which can be given in a variety of units depending on the problem. Usually, you’ll see R given as:

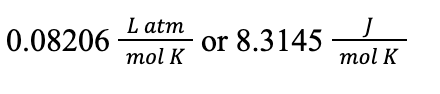
The trickiest thing about using the ideal gas law is units—you always want to make sure that the units of your pressure, volume, and temperature match the units of the gas constant you are given, otherwise your calculation will be incorrect.

At first, the ideal gas law might seem overwhelming because it contains many variables, but it can usually be simplified by eliminating variables that aren’t changing in the problem you’re trying to solve. This often happens when two variables are changing but the others are not. Let’s look at two examples of the ideal gas law in action.

Example 1: Amount of oxygen in a cylinder

A gas cylinder containing O₂ is used to help a hospital patient breathe. The cylinder contains 5.0 L of O₂ at 7.0 atm. The cylinder is kept in a room at 28 °C. How many moles of gas are in the cylinder?

This problem is an example of how units are key to calculations with the ideal gas law. The temperature unit given in the problem statement (28 °C) does not match the unit in the value given for R (K). So, our first step should be to convert 28 °C to temperature in Kelvin:

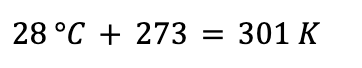
Now that we have the temperature in the correct units, we can use the ideal gas law. We want to know how many moles of gas (n) are present in the cylinder, so first we rearrange the equation for the ideal gas law to solve for n:

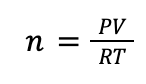
With this rearranged equation and our converted temperature, we can plug in the values from the problem statement:

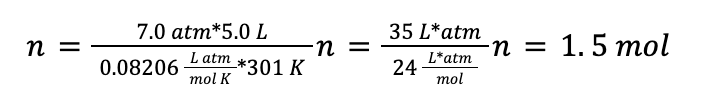
Example 2: Compressing a gas with a piston

A container containing 5.00 L of N₂ gas at an initial pressure of 0.500 atm is compressed using a piston to a final pressure of 2.00 atm. The temperature of the container is held constant. What is the final volume of the gas?

This problem is a good opportunity to eliminate variables that aren’t changing to simplify our calculation. Notice that the problem statement tells us that the temperature is held constant throughout the compression process. This means that we can ignore the T variable in the ideal gas law. The problem statement also implies that the amount of gas (n) does not change, since the gas is contained in a cylinder and does not escape, so we can eliminate n. Finally, since we have eliminated these variables, we can also eliminate R. Overall, this gives us the following equation:

First, we want to rearrange this equation to solve for the final volume (V₂):

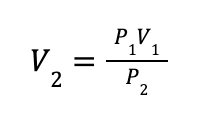
Then plug in the values from the problem statement:

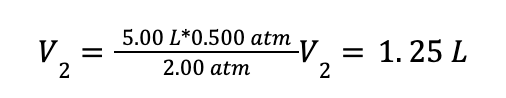
If you’re thinking—"whoa, where did the P₁V₁ and P₂V₂ come from?”—don’t worry, we’re still using the ideal gas law. In this problem, we are given an initial and final pressure and we are asked to find the final volume. We know that the number of moles and the temperature don’t change, so we know that the nRT on the right side of the ideal gas law remains constant. Knowing this, we could perform the following calculation using the initial pressure and volume:

At this point, we know that because nRT stays constant, we could also write the following expression for the final pressure and volume:

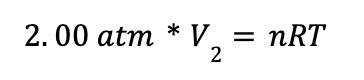
We can then set the two sides of the expressions equal to obtain:

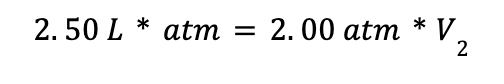
This expression is equivalent to the calculation we used above to obtain the result V₂ = 1.25 L.