In this blog post, we explore the four quantum numbers, which allow us to describe the properties of each electron within an atom. According to the Pauli Exclusion Principle, no two electrons can share the same combination of quantum numbers. A carbon atom has six electrons, for example, and each of these electrons can be described by one of six unique sets of quantum numbers.
The four quantum numbers are as follows:
- The principle quantum number (n)
- The orbital angular momentum quantum number (l)
- The magnetic quantum number (ml)
- The electron spin quantum number (ms)
The principle quantum number (n = 1, 2, 3, …) describes the shell in which an electron resides, with n = 1 describing the first shell, n = 2 describing the second shell, and so on. You can also think of n as a measure of distance between an electron and the nucleus. For example, because the second electron shell of an atom is further away from the nucleus than the first electron shell, an electron with n = 2 is further away from the nucleus than an electron with n = 1.

The orbital angular momentum quantum number (l = 0, 1, 2, …) describes the shape of the orbital in which an electron resides. Each value of l indicates a specific s, p, d, or f orbital. The s orbital has l = 0, p has l = 1, d has l = 2, and f has l = 3. Although l can technically be any nonnegative integer, you will probably only encounter l = 0, 1, 2, or 3 in your general chemistry studies. When determining l for a given electron, it’s helpful to note that l cannot be larger than n – 1. If an atom has three electron shells for example (n = 3), then valid values for l are 0, 1, and 2.
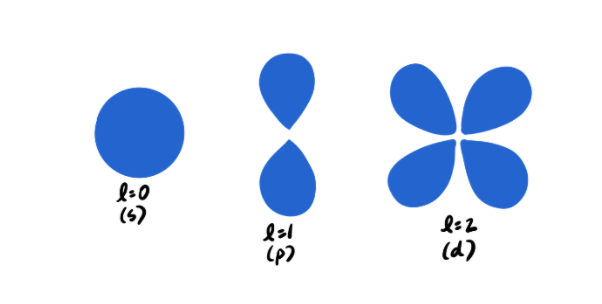
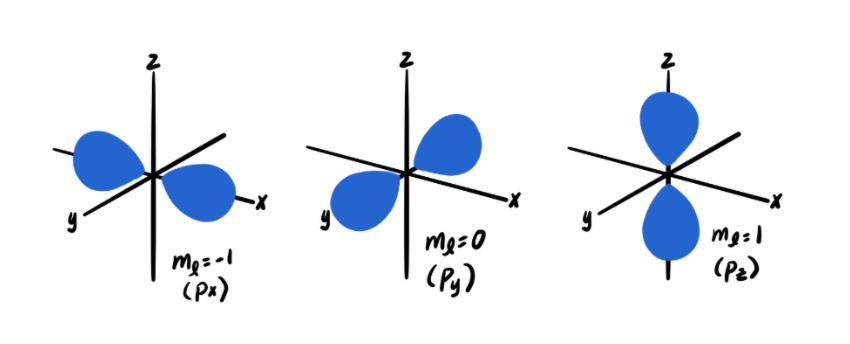
The magnetic quantum number (ml = …, -2, -1, 0, 1, 2, …) describes the spatial orientation of the orbital in which an electron resides. There are three orientations of the p orbital, for example (x, y, z), which are described by three magnetic quantum numbers (ml = -1, 0, 1). You may recall that a given orientation of an orbital is also called a subshell (e.g. the p orbital has three subshells).
The electron spin quantum number (ms = -1/2 or 1/2) describes the direction of an electron’s spin and does not depend on another quantum number. An electron with ms = 1/2 is said to have “spin up,” while an electron with ms = -1/2 is said to have “spin down.” There are only two possible values for ms because only two electrons can fit in a given subshell.
To summarize, this table presents the allowed quantum numbers for n = 1, 2, 3, and 4.
|
n |
l |
ml |
|
1 |
0 |
0 |
|
2 |
0 |
0 |
|
1 |
-1, 0, +1 |
|
|
3 |
0 |
0 |
|
1 |
-1, 0, +1 |
|
|
2 |
-2, -1, 0, +1, +2 |
|
|
4 |
0 |
0 |
|
1 |
-1, 0, +1 |
|
|
2 |
-2, -1, 0, +1, +2 |
|
|
3 |
-3, -2, -1, 0, +1, +2, +3 |
At some point, these rules break down. For example, Plutonium is in the seventh row of the periodic table (n = 7), and its electron configuration is [Rn]5f67s2. The only orbitals present are s, p, d, and f (l = 0, 1, 2, 3), yet our rules suggest that l can go up to 7 – 1 = 6 (the g orbital). What gives? The frustrating reality is that the idea of quantum numbers only works for smaller atoms; more complicated models are necessary for describing larger ones. On the bright side, you will likely not be tested on such a case in your general chemistry studies.

Comments