Have you ever wondered where the formulas for volumes that you studied way back in geometry come from?
It turns out that these formulas for volumes come from calculus! In fact, today I’ll talk about a very cool application of integrals that allow you to find the volume of any shape that can be made revolving a curve horizontally (around the -axis) or vertically (around the -axis).
Here are a couple of examples:
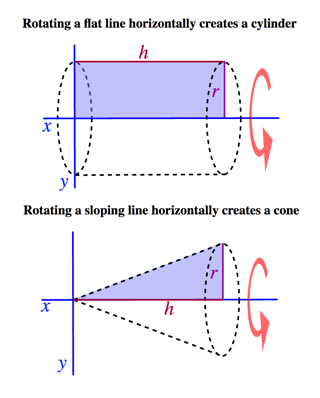
Solids that are created this way are known as solids of revolution.
The Basic Idea
The general formula for the volume of a solid of revolution around the x-axis is the following:
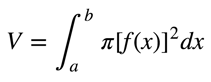
Here, V is the volume we are interested in, a and b represent the minimum and maximum -values of the curve that we are interested in revolving, and f(x) is the equation of that curve.
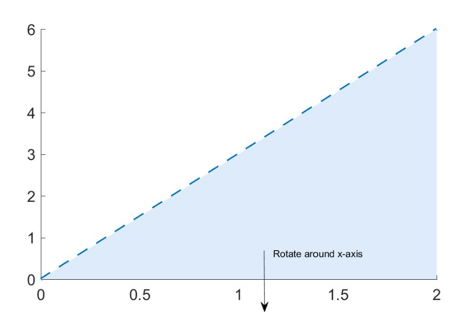
Let’s do a simple example: let’s take the graph y=3 . x of from x=0 to x=2 (shown below) and rotate it around the x-axis. As you can work out in your head or on a piece of paper, this will create cone of height 2 and radius 6.
By using the formula above, we see that the volume is:
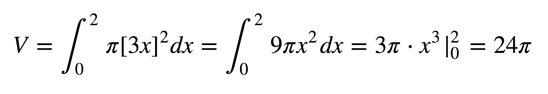
We can double-check that this is what we would get by using the standard formula for the volume of a cone:
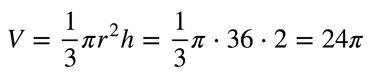
They match!
Rotating Around the Y-Axis
You might also see a variation of this problem in which the solid is generated by revolving a line or curve around the y-axis instead of the x-axis.
In this case, the formula changes slightly:
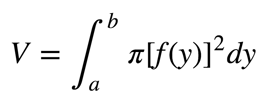Now, the integral is with respect to the function y in and the bounds a and b refer to the minimum and maximum values of y.
Let’s consider the example of the same line as in the previous part, but now rotated around the y-axis:
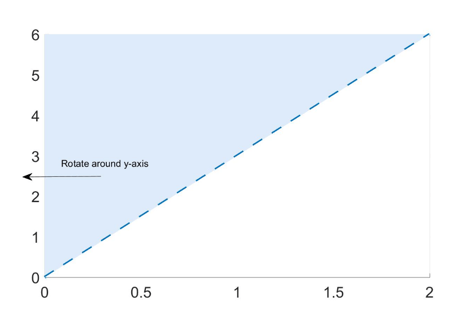
To use the formula above, we must first rewrite the equation for the curve in terms of y:
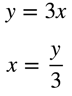
Also, we note that the bounds are now a = 3(0) a = 0 and b = 3(2) = 6. Now, we are ready to substitute:
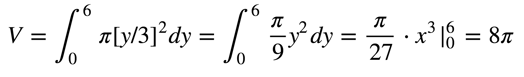
Again, you can check that this is the same volume that you would get if you used the volume-of-a-cone formula.
Hollowed-Out Solids
There’s one more twist that you might see when you solve these kinds of problems, and those are solids that are rotating the area between two curves.
Here’s an example of that. We are rotating the area between the curves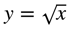 
and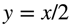 
around the x-axis. Can you visualize the resulting volume? It’s an irregular 3D shape that looks like a dome with a cone taken out of it.
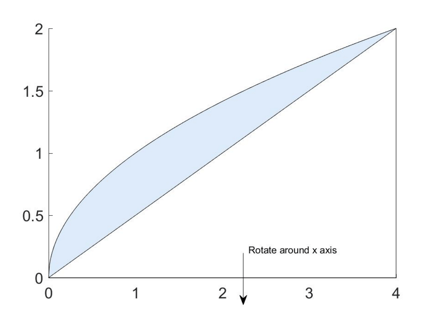
How do we find the volume of this irregular shape? Simple. We subtract the volume generated by rotating the “upper” curve and the volume generated by rotating the “lower” curve.
Here’s what that looks like:
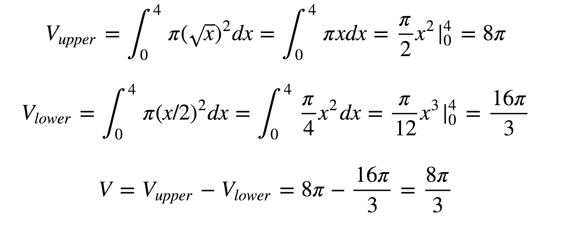
Conclusion
We’ve covered a powerful application of integrals, finding the volume of solids of revolutions. This is a really useful and simple technique – not only can we use it to derive formulas for the volumes of simple shapes like cones and cylinders, but we can use it to find the volume of all sorts of irregular 3D shapes that we don’t have simple formulas for!
Comments