If you type √5 into your calculator, it’ll output something like 2.2360679775. But how did your calculator find that answer? Is there any way you could have found it by hand?
To find an answer, we’ll need to use a concept found in calculus called “Taylor approximation.” In this post, we’ll focus on the problem of computing √5, and will define “Taylor approximation” along the way.
First, let’s clarify what we mean by “computing” √5. Unfortunately, there’s no hope of writing out the exact value of √5 as a decimal, because its decimal expansion stretches on forever. Even your calculator can’t compute √5 exactly: the answer 2.2360679775 output by your calculator is accurate to 10 decimal places, but it’s still only an approximation. So ,when we say “compute √5”, what we really mean is “find a very good decimal approximation for √5.”
1. Zeroth-Order Approximation
One very basic way of approximating √5 is to say: “Well, 5 is close to 4, so √5 should be pretty close to √4 = 2. In other words, 2 is a pretty good approximation of √5.” And indeed, the approximation √5 ≈ 2 is acceptable: the error in the approximation (that is, the difference between the approximation and the exact value) is only 0.2360679775… = 2.4… × 10-1.
What’s really going on in the above argument? One enlightening way of thinking about it is using the function f(x) = √x. Then, we’ve claimed that since 5 is close to 4, it should also be true that f(5) = √5 is close to f(4) = √4 = 2. We can see this on a graph of f(x): the point (5,√5) on the graph of f(x) is close to the point (5,2).
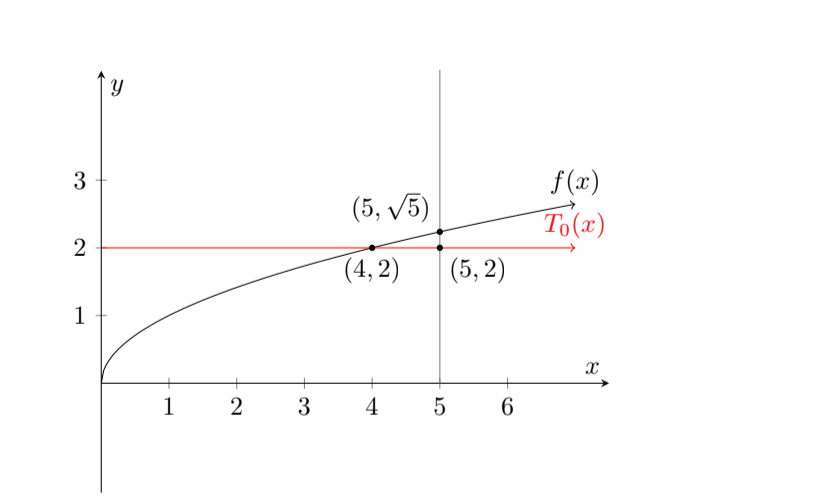
The constant function T0(x) = 2 is called the zeroth-order Taylor approximation to f(x) centered around x = 4. (We’ll see where this terminology comes from soon – have patience!) Its graph is the red horizontal line pictured above. For values of x close to 4, the function T0(x) is a good approximation for f(x). This is useful because T0(x) is much, much simpler to compute than f(x)!
2. First-Order Approximation
In the previous section, we approximated the function f(x) = √x (for values of x close to 4) using the constant function T0(x) = 2. We can do better by instead using a linear function T1(x).
This function T1(x) is called the first-order Taylor approximation to f(x) centered around x = 4. It’s sometimes alternatively called the linear approximation or tangent-line approximation. Geometrically, the graph of T1(x) is just the tangent line to the graph of f(x) at the point (4,2).
To find the function T1(x), we first use the Power Rule to find that:
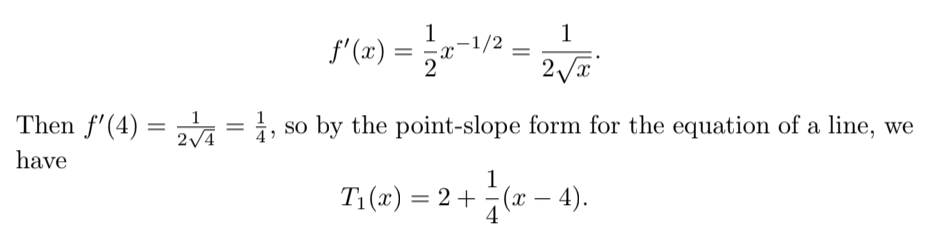
Here’s a graph of f(x), T0(x), and T1(x). You can see that for values of x near 4, the function T1(x) is even closer to f(x) than T0(x) is:
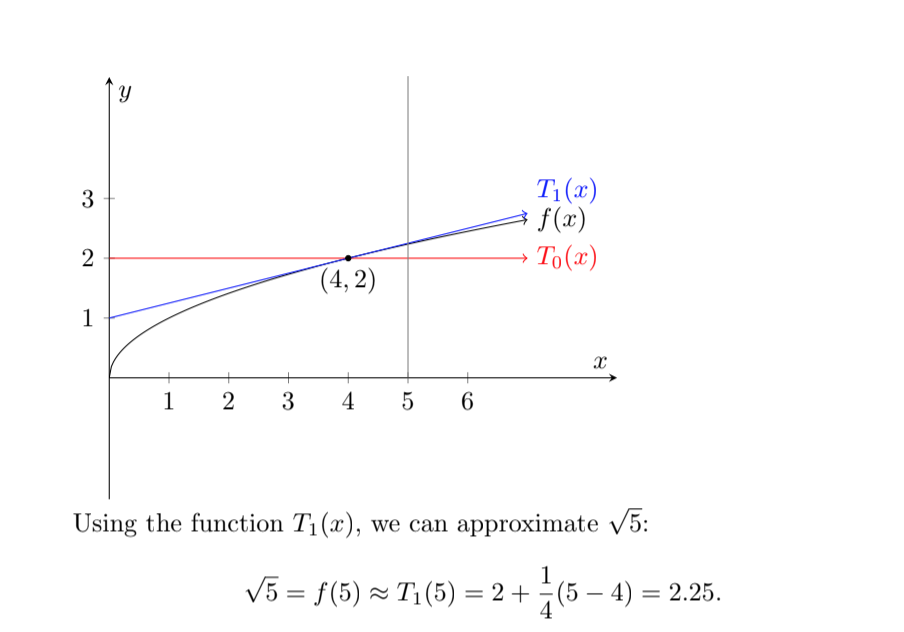
The error in this approximation is 1.3…× 10-2. That’s much smaller than the error in the zeroth-order approximation!
3. Higher-Order Approximation
The idea of Taylor approximation is to continue the pattern laid out in the previous two sections. We’ll get a sequence of functions T0(x),T1(x),T2(x),… that are all approximations to f(x) for values of x close to 4, with each approximation more accurate than the last.
In general, the function Tn(x) is called the nth-order Taylor approximation to f(x) centered around x = 4. It is a degree n polynomial, and to find it you need the values of f(4),f′(4),…,f(n)(4).
Here’s a graph of T0(x), T1(x), T2(x), and T3(x) and a small table summarizing what happens when you use those functions to approximate √5 = 2.236067977….
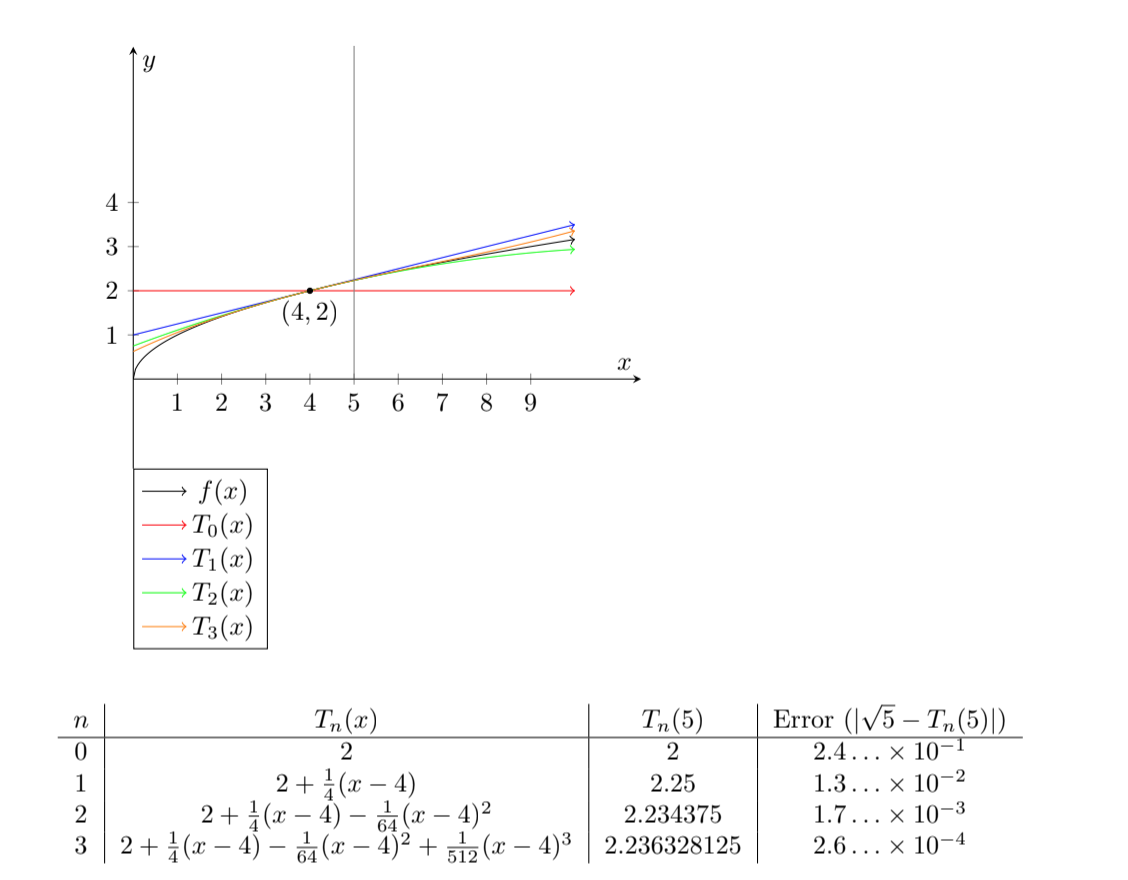
One of the most important theorems in calculus is Taylor’s Theorem, which not only tells us how to find all of the functions Tn(x), but also guarantees us that the error |Tn(x) - f(x)| can’t be too large.
Mathematics – from high school math to graduate school math – is one of our most frequently requested subjects. Teaching math is notoriously difficult and we maintain a staff of mathematicians who are committed to the art of teaching. There is no course or standardized test that we do not have extensive experience teaching. We work with students who loathe math and students who love it, students who haven’t done math in a decade and students who work on mathematical problems every day. Many of our students work with tutors to address courses or exams – such as Geometry, Linear Algebra, Differential Equations – but we also work with students looking to explore more advanced or unconventional topics (like the mathematics of poker, or algrabraic topology, for example).
Have a passions for Mathematics? Check out some of our other blog posts below!
Comments