Welcome back to our series of posts on building your physical intuition for E+M! In this series, we’ve looked at some physical reasoning behind Coulomb’s law, imagining point charges as radiating electric field, and saw that the Biot-Savart law gives an analogous result for magnetic fields. We then took the intuition that we’d developed for point charges and currents, and scaled it up to look at long wires and infinite sheets of charge and current.
Up until now, we’ve focused on the magnitude of the electric or magnetic field. How can we easily use our physical intuition to determine the direction of the field as well?
Use the geometry of the problem!
Often, the first step in figuring out how to solve a problem is to look at the information the problem gives you! You should try to practice the strategy of examining the pieces of information that a problem gives you, and using them as a starting point to figure out how the pieces fit together. This strategy is extremely useful when thinking about physics intuitively, or working through the quantitative sections of the SAT or GRE.
Let’s start with a simple example: finding the electric field at point P due to a point charge at point O. The only relevant vector in the problem is the displacement r, which points from the charge at O to our observation point at P. We already know that the electric field points directly towards or away from a point charge, but this is a subtly different way of thinking about it. The field is either parallel or anti-parallel to the displacement r because that is the only direction in the problem; where else could the field possibly point?
What if there is more than one relevant direction in a problem? Consider the magnetic field due to a wire carrying a current I. Here, I made the current I a vector because we need to consider its direction along with the displacement r. Here, the answer is the cross-product I x r, which is perpendicular to both I and r. Again, we find out something that we already know, that the magnetic field curls around a current-carrying wire. This time, let’s think of it this way: there are two vectors in the problem and our answer needs to be a vector, so a logical choice is the cross-product of the two vectors.
Hopefully, this strategy should remind you of dimensional analysis. The two techniques share a similar deductive spirit. Using dimensional analysis, you recognize that you need to put together an acceleration and a length to find a time, for example, and you realize that you can only combine them in certain ways to make the units work out. Here, you recognize that you need to put together either one or two vectors to form another vector, and there are only certain ways you can do that.
The Cross-Product: A very useful concept!
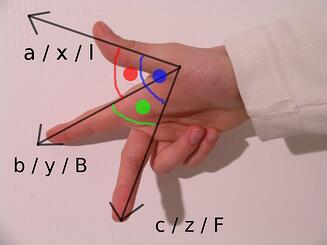
If you are not familiar the cross-product, the concept is simple: Say c = a x b, where a, b, and c are all vectors. The vector c is perpendicular to both a and b, and its magnitude is given by c = ab sin(θ), where θ is the angle between a and b. To figure out the specific direction of c relative to a and b, you can use the familiar right hand rule: If you hold your hand as pictured above, then a points along your pointer finger, b points along your middle finger, and the cross-product c points along your thumb.
The choice to use a cross-product seems arbitrary. How can I decide if I should or not?
So, one vector in the problem means the answer is parallel or anti-parallel to that vector, while two vectors in the problem means the answer is parallel or anti-parallel to their cross-product?
As with many sweepingly general questions, the answer is yes but no. Yes, in that the rule is very commonly true. No, in that there are many exceptions, and simply committing a rule of thumb to memory without thinking about why such a pattern exists misses the point (and the fun) of science.
Cross-products tend to arise when two physical quantities that both have directions interact, and the result is some effect that also has a direction. By contrast, when you only have one physical quantity that has a direction, it tends to create effects that point either along with or opposite to its direction. This statement was abstract and a bit vague, so let’s illustrate it with some examples.
Consider an electron moving in either a magnetic or electric field. For the magnetic field case, the Lorentz force law tells us that the force depends on the direction of the magnetic field relative to the direction of the electron’s motion. Since we have two quantities with direction – the field and the electron’s velocity – interacting, the next logical step is to take their cross-product. If the electron were moving in an electric field, however, the force would only depend on the direction of the electric field and the magnitude of the electron’s charge. Since nature doesn’t care where the electron is moving, the electric field should only create a force parallel or anti-parallel to its own direction.
A useful analogy between E+M and mechanics
We can draw an analogy here between electric versus magnetic fields on the one hand, and linear versus rotational motion on the other. In both cases, there are deep similarities between the two concepts being compared. We’ve already explored some of the parallels between electricity and magnetism, and you have probably noticed that linear and angular motion involve several of the same quantities – velocity, momentum, mass/moment of inertia, force/torque – arranged in analogous ways.
For electricity and linear motion, we are dealing with fields and motion relative to a point. What is the electric field due to this collection of point charges? The car starts at this point and accelerates eastward, so what are its velocity and displacement? The point charge and the car’s origin have no direction; they simply exist at a given location. Here, all the calculations generally involve motion/acceleration/fields/forces parallel to some direction or another; this is why we can decouple vertical from horizontal motion when considering the flight of a cannonball, for example.
For magnetism and rotational motion, the fields and motion depend intimately on some vector. What is the magnetic field due to a current moving in this direction? What is the angular momentum of a top spinning around that axis of rotation? In these cases, we need to know where the current is pointing relative to our observation point, or how all the bits of mass in the top are moving relative to the top’s center in order to answer the question. In these contexts, the cross-product – the simplest way math offers to combine two vectors representing different physical quantities to form a new vector – is ubiquitous.
Some less obvious E+M examples
To drive home the idea of considering the vectors involved to find an electric or magnetic field, let’s return to the example of an infinite plane of charge or current. We’ve already seen that the magnitude of the electric or magnetic field produced by the infinite plane does not depend on the distance from the plane, but what about the direction of the field?
Let’s first think about the vectors in the problem. How do you characterize the direction of a plane? Consider describing the direction of the surface of a table. There are an infinite number of vectors that lie in the plane, just as you can put your pencil on the table and point it north, or east, or south-by-southwest, etc. The best way to describe the table is to say that it is horizontal. That is, no matter how you place your pencil, it will always be perpendicular to vertical. Mathematically, then, the best way to describe the orientation of a plane is to give the direction of its normal vector, the vector the sticks straight out of the plane at a 90 degree angle all around.
For an infinite plane of charge, the electric field must point either parallel or anti-parallel to the only direction in the problem. That is, the electric field at all points must point directly toward or away from the plane, depending on the sign of the plane’s charge. Intuitively, this makes perfect sense. Imagine flying in an airplane above a perfectly smooth sea. North, south, east, and west are meaningless to you, and the only directions you can distinguish are up and down.
For an infinite plane of current, you have the direction that defines the orientation of the plane and the direction of the current within the plane. If we take the cross-product of these two vectors, we find that the magnetic field flows parallel to the direction of the plane, but perpendicular to the direction of the current. Again, this makes perfect intuitive sense. Picture boxes in a warehouse sliding along a track of rollers. For each roller, the surface of the cylinder spins around the roller’s center, much like a single current-carrying wire creates a field that wraps around the wire. Placed closely enough together, though, the rollers create a smooth horizontal motion, and the surface of one roller comes up to meet the box as the surface of the previous roller drops away. Analogously, if you imagine the infinite plane of current as a flat collection of wires stuck together, then the wires together create a magnetic field that flows smoothly along the surface of the plane, while the components of the individual fields that point toward or away from the plane are cancelled away.
Two important tools in your geometric intuition toolbox
Looking at the vectors given to you in a problem is sometimes not enough to give you your answer. Consider a ring of charge, an electrified donut, and you need to find the field in the center of the hole. Using the analysis we described above, we might say that the electric field points straight out of the hole, perpendicular to the diameter of the ring. This answer, however, is incorrect. In addition to considering the geometry of the problem, we must also consider its symmetry!
In the next post, we’ll explore how symmetry and geometry together can be a powerful combo for helping you reason through physics problems.

Comments