
As a physics tutor, I repeatedly see students overlooking the need to integrate knowledge from different parts of their science education. This post focuses on my attempt to show how a simple concept emerges again and again in many places, from your first semester of high school physics to the cutting edge of research.
In the first post, we talked broadly about the role of analogy in science. In the second post, we launched into examples by discussing the kinetic and potential energies of a mass on a spring, a canonical example from high school mechanics. In this post, we'll move from mechanics to some electricity and magnetism!
How is an electron in a circuit like a mass on a spring?
In the last post, we thought about what happens when you push a mass that is attached to a spring. You stretch or compress the spring, and the work that you do is converted to potential energy stored in the spring. Can we find a similar idea in the world of electrical circuits?
Picture a basic circuit: two parallel metal plates with a wire connecting the outside face of one plate with the outside face of the other. This is the simplest picture of a capacitor. Hold this picture in your mind just beside the mass on a spring.
The capacitor is initially uncharged; the plates and wire are just electrically neutral chunks of metal. Similarly, we can imagine that the spring is initially relaxed; neither stretched nor compressed, the spring is exactly as long as it wants to be.
Now, we take one electron from the left plate, move it through the wire, and put it in the right plate. We’re not concerned with how exactly we are moving the electron; we will say ”and yet it moves” and go on. Now, the left plate has a net positive charge (there’s a proton in a metal nucleus somewhere that is missing its cancelling electron) and the right plate has a net negative charge (there’s an extra electron without a proton to cancel).
This charge imbalance creates an electric field between the two plates, which creates a voltage difference between the two sides of the capacitor. This voltage tries to make a current flow through the wire, trying to push that electron back to the left plate from whence it came (hence the negative sign). The more charge we move from the left plate to the right, the greater the electric field and the voltage difference become, and the more the capacitor wants to create a current to restore the system to equilibrium. The magnitude of the voltage is given by
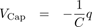 ,
,
where q is the net voltage on plate and C is the capacitor’s capacitance – essentially the capacity of charge it can hold for a given voltage. Notice how similar the voltage across a capacitor is to the force of a spring:

Moving charge from one plate to the other is precisely like compressing the spring – the farther we push the spring, the harder the spring pushes back against us!
The spring and capacitor act the same – so what does that mean?
We should not be surprised, then, that when we calculate the energy stored in the capacitor – the energy we put into the capacitor by moving each electron “uphill” against an opposing voltage – we find
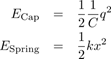 .
.
The analogy is clear – x is replaced by q and k is replaced by 1/C. This makes perfect sense – a stiffer spring and a smaller capacitor both resist more strongly if you push them away from equilibrium, and both store more energy than a more flexible spring or larger capacitor for the same push distance.
Does velocity also have an electrical analog?
In our previous post, the potential energy of a spring and the kinetic energy of a mass in motion formed a complementary pair. We’ve found that a capacitor is an electrical analog for a mass on a spring, so can we find a similar analog for a mass in motion?
In the capacitor example, moving small bits of charge from one plate to the other was analogous to pushing the mass to one side against the spring. That analogy suggests that if we want to find an analog for velocity (the rate at which the mass’s position changes), we should think about current (the rate at which we move charge through the wire).
Imagine a simple coil of wire – the wire comes in from one side, takes a few turns (perhaps around a metal core), and goes out the other side. This is the basic picture of an inductor. We know that charges in wires create magnetic fields. If you pass a current through the wire, it creates a magnetic field that runs through the center of the coil, pointed straight down the screw’s shaft in the picture above. If the current suddenly stopped flowing, then the magnitude of the magnetic field would also go to zero.
We also know, however, that changing magnetic fields can influence charges in loops of wire. If the magnitude of the magnetic field inside the coil were to quickly go to zero, then it would induce a voltage in the coil. The coil both creates the magnetic field and reacts to it – this is called self-inductance. Lenz’s law tells us that the voltage induced by the changing magnetic field gives rise to a current that tries to counteract the change. In other words, the coil’s self-inductance tries to keep the current flowing. This is inertia! Imagine pushing a full grocery cart and trying to come to a complete stop – the cart’s mass tries to keep it moving, just as the coil’s self-inductance tries to keep the current flowing!
Mathematically, the voltage across the inductor, the loop of coil, is
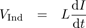 ,
,
where L is the coil’s self-inductance and dI/dt means “rate of change of I.” Notice that this expression looks just like the expression for force that we used last time:
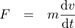 .
.
Again, we are not surprised to find that if we repeat the math from the last post, we find
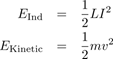 .
.
The analogy between mechanical motion and the flow of electricity holds again! The self-inductance L and mass m both provide inertia, which resists our attempts to change the current I or velocity v suddenly.
Put the two halves together
Now we see that loading charge onto a capacitor is analogous to compressing a spring, and flowing current through an inductor is analogous to setting a mass in motion. Can we put the two halves together?
Recall that when we set the mass on a spring moving, it formed an oscillator. The mass’s inertia compressed the spring, creating potential energy. The compressed spring then pushed the mass back into motion, converting the potential energy into kinetic energy. On and on it went, the mass oscillating back and forth, interchanging energy seamlessly between potential energy in the spring and kinetic energy in the mass.
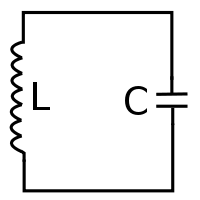
The same thing happens if we wire an inductor and capacitor together. This is called an LC circuit, and is shown above. While currently flows through the circuit, energy is stored in the inductor – the mass moves to the left. Eventually, the current builds up enough charge in the capacitor that the voltage across the capacitor stops the current – the spring brings the mass to a stop. The capacitor discharges, sending current back through the inductor, and the entire process repeats.
This circuit, as much as a mass on a spring, is an oscillator! If the characteristic frequency of the mass on a spring is
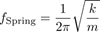 ,
,
then we shouldn’t be at all surprised that the LC circuit resonates at a characteristic frequency of
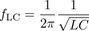 .
.
In fact, this is how radios worked before digital electronics. There are electromagnetic waves of all different frequencies zipping through the air around us (light is one example), but we want our radio to respond to one frequency only. Just as you can only make a mass on a spring oscillate if you shake it at the right frequency, only radio waves of the right frequency will be picked up by a radio’s LC circuit. To tune to a different station, you just change the value of C inside your radio with a knob, much like you might replace the spring with a stiffer or more flexible one to change the mass’s oscillation frequency.
Next time – pushing further!
Now that we’ve seen the same ideas pop up in two different places, let’s see if we can push the analogy further. Tune in next time, when we’ll drop the wires, coils, and plates, and dig in to some interesting E+M!
Comments