Learning to take standardized physics exams, like the AP Physics exam or the SAT Physics Subject Test, is not unlike trying to become fluent in a foreign language. Both follow highly idiosyncratic logic and are best learned through practice. (And believe it or not, standardized physics exams have less to do with physics than physics aficionados would like.) Now before you combust, hear me out. I’m not saying that the tests don’t contain physics, or that understanding physics won’t help you; I’m saying that it is only one of many factors in these exams.
But don’t worry! As your trusty advanced physics tutor in New York, I’m here to help. In this post, I’ll talk about some test-taking strategies that are unique to physics standardized exams. These are especially useful when you’re stuck on a problem, or feel short on time. These techniques are often not taught in elementary physics courses, but you’ll find them tremendously helpful when the big test day comes.
Solving problems by eliminating solutions
The beauty of multiple-choice exams is that they do not require you to actually solve the problem. If you’re able to eliminate at least one answer choice, it’s in your best interest to guess at random, or deduce based on the choices given.
If you had to do every problem completely, ETS tests would primarily be tests of speed. So don’t. No, the real world does not involve multiple choices. If you are an engineer trying to design a voice-modification system, you will not be simply given a set of four choices of this sort:
The answer choices in this question might seem outlandish, but, as we will soon see, often times you will have many outlandish answer choices. It’s just a question of learning to identify which choices are outlandish.
Technique #1: dimensional analysis
The first technique I’ll introduce is dimensional analysis, which we also occasionally refer to as unit analysis, or forces are not measured in meters (well, at least not directly). As the name suggests, this approach primarily consists of ensuring that expressions for physical quantities such as forces are in the appropriate units. An example of an exam question might be something like this:
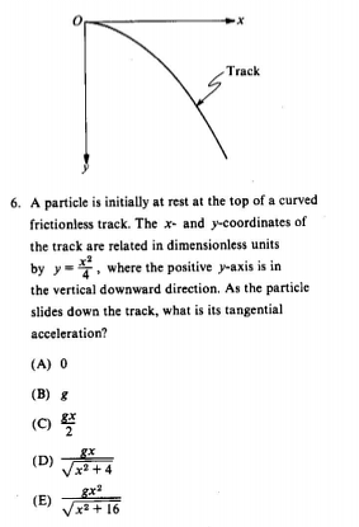
The above problem comes from the 1986 Physics GRE exam. Now, some clever readers might know how to solve the problem by using free body diagrams and the restriction . Some advanced readers might recognize the opportunity to use the Lagrangian to solve it. Both of these methods prove somewhat tedious. The tangential acceleration must be in units of acceleration, yet answer choices (C) and (E) are clearly in units of acceleration*distance. Therefore answer choices (C) and (E) in this problem are as nonsensical as suggesting bananas in the voice modulators problem. This leaves only (A), (B) and (D).
The object is obviously accelerating because if we placed it at some point on the track other than the very top, it would have to start moving downwards, thereby making (A) incorrect. If we placed it at the top, it would not accelerate at all: therefore, (B) is out. One could also eliminate B by noting that the object is not in free fall. Therefore, we arrive at the answer choice (D) without having to actually do any computation.
Remember this tip: in dimensional analysis, units should cancel out. Any time you have an exponent, logarithm, trigonometric, or otherwise non-polynomial function used to represent a physical constant, its argument must be dimensionless. Those who have studied Taylor series will know that these functions can be written out as an infinite polynomial expansion. Therefore, if you take the exponent of a length, you are adding units of meters to meters2, meters3, etc. and that does not make physical sense.
Technique #2: Limiting Behavior
Let’s look at the same problem again, this time with a new technique. What would the acceleration be like for large x (say x=1,000,000m)? Note that a parabola at that point would be practically vertical at that point: the particle would essentially be in free fall (its acceleration would have magnitude g). Answer (A) is therefore completely wrong. Answer (B) is right in this limit, but wrong because it requires a particle to be in complete free fall. Answers (C) and (E) will produce accelerations of the order 9.8*106 m/s2, which is in clear disagreement with basic physical intuition.
For those who have taken elementary calculus (or, in some cases even pre-calculus), you may recognize this as taking the limit as a variable goes to infinity. This can also be applied to variables going to 0, provided you have some idea of how the system should behave at such a limit. This technique is also a handy way to work on inclined plane problems if one is rusty on how to deal with their geometry. To determine when a cosine or a sine is more appropriate, simply take the angle in question to its 0° or 90° limit and ask yourself what you would expect to happen.
Technique #3: Limiting Values
This technique is slightly more subtle than the previous two. Here, we make the statement that “the value in question must be greater than x and less than y”. Looking at the question above, it is safe to say that the acceleration is always greater than 0 (except at the very top), as an object put on any hill will tend to slide or roll downwards. Next, we note that because there is a surface underneath the body, the body’s acceleration must be less than g. The only answer choice for which this is always true is (D). This last technique might be a little bit tricky when it relies on physical intuition, which is very easy to misuse.
There you have it, three techniques that should make you a faster and more effective test taker on the standardized physics exams, whether it’s the GRE Physics subject test or the AP Exams exam. No matter how knowledgable you are at physics, you have to learn to treat physics standardized tests as a whole different species of animal. Here are some other blog posts on physics you may find useful, with problem solving tips, and using analogies to understand physics concepts.

Comments