All shapes, from strings to bridges to carrots, resonate
You’re having breakfast in the kitchen when you start to hear a series of slow and repetitive thuds – someone is coming down the stairs. Without having to ask or look up, you can instinctively guess who it is. That’s because the cadence and volume of one’s footsteps is unique from person to person, depending in a significant way on the geometry of their gait and body structure. Of course, it isn’t too surprising to suggest that geometry and sound are interrelated; you can hear the difference between strings of different thicknesses and drums of different widths. The shapes of these instruments affect the frequencies they resonate at.
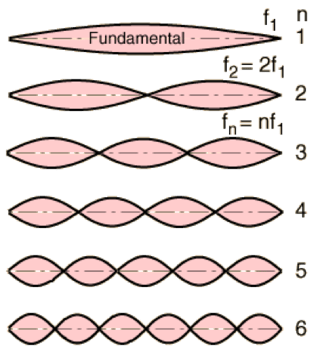
What might be more surprising to discover is that every shape resonates, not just musical instruments. Bridges, for example, can resonate when the wind hits the right note, as the famous collapse of the Tacoma Narrows Bridge reminds us. For shapes that are more complicated than strings, the resonating patterns can be quite complex.

However, these resonations also have a frequency – a single number which corresponds, musically, to the note produced. The collection of all the resonate frequencies provides a sort of summary of that shape as a list of numbers – the possible musical notes it can produce. This collection of notes is called the spectrum of the shape.
Can you hear the shape of a drum?
It wasn’t too long before the question was asked: “can you hear the shape of the drum?”. In other words, if two shapes have the same spectra, must they have the same geometry, or is some information lost when you only record their musical frequencies? Put another way, can you tell who I am simply from the sound I make when I knock the door? This fascinating conjecture is one of many questions in the field of spectral geometry, which investigates the geometric significance of resonate frequencies.
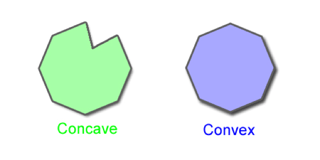
When, in 1992, mathematicians produced two different drums with the same spectra, the question was resolved in the negative. Yet, hope is not lost. You can hear the shape of a drum if you know the drum is convex, and that its sides are smooth enough. And regardless of the technical restrictions necessary for the music of a drum to completely determine its dimensions, there is clearly a lot of geometric information hiding in the notes.
Music as Applied Mathematics
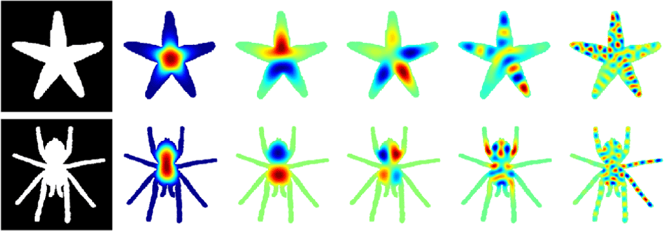
In recent years, mathematicians have developed ways to use the spectrum of a shape for the computational tasks of shape comparison and recognition, with the intuition being that similar shapes generally produce similar sounds. The advantage of this spectral method is that it is much simpler to compare two lists of numbers than it is to compare two large geometric objects. This is an ongoing area of research producing new techniques that are starting to be applied in areas like medical imaging and neuroscience, where the complex, three-dimensional forms of human life resist the classical geometry of triangles and trapezoids.
Are you interested in connecting with a mathematics tutor, either in Boston or New York?
Craving more reading materials on mathematics? Read on below!

Comments