Mathematical proofs are what make math objective: while you could find a few examples that "prove" a mathematical statement, it is often more important to write a rigorous proof that holds true in all cases. Mathematicians have a few methods in their toolkit to tackle different proofs. In this post, we will learn how to write a proof by contradiction.
pExample 1: Prove that √3 is irrational.
We will begin by letting p be the statement “√3 is irrational". Since we will be proving this statement by contradiction, we will assume that the opposite of p, p, is true i.e. “√3 is rational". By definition, if √3 is rational, then there must be some pair of integers a and b such that:
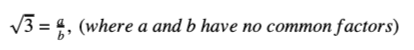
We obtain following expressions after squaring both sides of the equation (1):
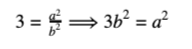If 3b2 = a2, then a2 (and consequently a) is divisible by 3. Therefore, we can say that a =3k for some integer k (which is the mathematical definition of being divisible by 3). Thus, we have that:
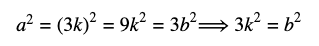
Equation (3) tells us that b2 (and consequently b) is divisible by 3. Yet, according to our statements in equation (1), a and b have no common factors. Can a and b have no common factors and also have a common factor of 3? No - this is a contradiction! Therefore, our initial statement p: “√3 is rational" is false, which proves that p: “√3 is irrational" is true. We have thus completed our proof by contradiction.
Example 2: Using proof by contradiction on the SAT/ACT
Proof by contradiction can also be used to tackle certain SAT/ACT math problems. Let’s look at a problem from the calculator section of an official SAT practice test:
We can solve this problem by checking each answer choice and using our proof by contradiction method. Let’s start with checking the first answer choice.
First, we let p be the statement: “−1 is NOT a solution to the inequality 3x−5 ≥ 4x−3". Now, for the sake of contradiction, let’s assume the opposite, p, is true: “−1 is a solution to the inequality 3x−5 ≥ 4x−3". We will then substitute x=−1 into the above inequality to check if p is true or not.
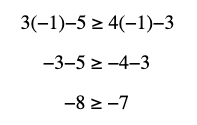
Note that we get that −8 ≥ −7 which is obviously a contradiction. Therefore, since p: “−1 is a solution to the inequality 3x−5 ≥ 4x−3" is false, then it follows that p: “−1 is NOT a solution to the inequality 3x−5 ≥ 4x−3" is true.
Hence, the correct answer is (A).
I recommend double checking the other answer choices just to be sure. Spoiler alert: none of the other choices give us a contradiction when we assume they are solutions to the inequality.
Final Thoughts
Proof by contradiction is one of the most powerful proof methods that mathematicians use routinely in their work. Notice that this methodology can be applied regardless of the difficulty of the problem. I often have my SAT/ACT students use this method on the multiple choice sections when they are stumped. This is one of the rare instances in life where being “wrong" is ultimately a good thing.
Mathematics – from high school math to graduate school math – is one of our most frequently requested subjects. Teaching math is notoriously difficult and we maintain a staff of mathematicians who are committed to the art of teaching. There is no course or standardized test that we do not have extensive experience teaching. We work with students who loathe math and students who love it, students who haven’t done math in a decade and students who work on mathematical problems every day. Many of our students work with tutors to address courses or exams – such as Geometry, Linear Algebra, Differential Equations – but we also work with students looking to explore more advanced or unconventional topics (like the mathematics of poker, or algrabraic topology, for example).
Check out some of our previous blog posts related to mathematics below!
Comments