
Welcome back to this series on thinking by analogy in physics! Check out our previous posts:
We talked generally about the role of analogy in science, then traced a simple idea – a mass oscillating back and forth on a spring – up through its appearances in classes on mechanics, electronic circuits, and electricity and magnetism. As a physics tutor, I frequently see students try to get through a physics class or study for the physics AP or GRE test through rote memorization alone. If I help them to pull back and to place their lists of equations within the broader context of recurring physical ideas, however, then they are much better able to retain and use the material they learn. Through each post in this series, I'm demonstrate this technique for you: one simple idea can reappear again and again in different, yet analogous, forms.
In the last post, we ended with the discovery that electromagnetic radiation – the visible light that illuminates a concert stage, the radio waves that connect your cell phone to the world, or the microwaves that heat your food – is essentially just energy oscillating back and forth between electric and magnetic fields. Let’s pick up the thread there, and trace it down into the realm of quantum mechanics.
What makes quantum mechanics quantum?
In previous posts, we’ve discussed some weird and wonderful aspects of quantum mechanics. But what precisely makes quantum mechanics, well, quantum? Let’s explore that question by asking another question, one of the vexing issues that the advent of quantum mechanics answered: how exactly do electrons in an atom orbit the nucleus?
Picture the Rutherford model of the atom: electrons orbiting the nucleus like satellites orbiting Earth, perpetually accelerating inward. When a charge accelerates, it gives off electromagnetic radiation. This is how radio transmitters work: the tower is essentially one long wire through which the radio station alternately pushes and pulls electric current in time with the song it is broadcasting.
Why, then, does an electron not throw off radiation constantly as it orbits the nucleus, like a litterbug continually chucking empty cans from their car as they careen around an infinite curve? That radiation would leech energy away from the electron, causing it to spiral inward towards and eventually be captured by the nucleus.
We know that atoms, like those that make up you and me, exist, so this must not be the case. Why not? The answer is that both the electron’s orbit and the radiation it emits are quantized. To be quantized means to be composed of some countable number of irreducible pieces, which are called quanta (think “quantity ” or “quantify”). One such piece is called a quantum, which gives us the name quantum mechanics. To illustrate what quantization means, let’s imagine a quantum satellite and contrast it with its everyday classical counterpart.
Quantum vs. classical satellites
As a classical satellite orbits the earth, it feels some slight air resistance as it passes through the upper reaches of the atmosphere. This air resistance, essentially the act of continually shoveling air molecules out of the satellite’s way, exerts a drag on the satellite and slows saps its energy. The satellite falls lower and lower toward the earth, becoming more and more susceptible to air resistance, until it finally plunges to the ground, echoing the classical picture of an electron plunging into the nucleus.
How is our quantum satellite different? For a quantum satellite, both its orbit and the energy it loses must be quantized. A quantum satellite can only orbit at fixed heights. It can fly 100 miles above the ground, or 400, or 900, or 1600, or any n2×100 miles, but never at any height in between. (Why are orbits allowed at only heights of n2×100 miles instead of, say, every 100 miles? This relation comes from the fact that the satellite can gain or lose angular momentum in equally sized chunks, which is explained more fully here. The satellite must always have at least one chunk of angular momentum, which explains the minimum orbital height of 100 miles.)
A quantum satellite simply cannot exist in an orbit 200 miles above the earth, so there is no way for a quantum satellite to slip smoothly from 300 miles to 100 miles above the ground. Likewise, a quantum satellite cannot lose its energy gradually by plowing through a continuum of air molecules, but instead must release a burst of energy all at once.
Picture, then, a quantum satellite orbiting 400 miles up. It stays perfectly in its orbit, never disturbing a single molecule of the atmosphere. Suddenly, the satellite emits a burst of energy into the atmosphere equivalent to losing 300 miles of altitude, creating a spectacular sonic boom. Instantaneously, having lost 300 miles’ worth of energy, the satellite now orbits at 100 miles. There was no smooth slide downward; the satellite simply orbited at 400 miles one moment and at 100 miles the next.
What happens now that the satellite is 100 miles up? Nothing! There are simply no possible orbits under 100 miles and the satellite, constrained by quantization, cannot drift slowly downward.
THe bohr model
We now see the solution to the riddle of the atom! Electrons do not spiral into the nucleus because they, like the quantum satellite, can reach a lowermost orbit from which quantization will allow them to fall no farther. This model of the atom is called the Bohr model, and its introduction of quantization in 1913 foreshadowed the development of a fuller quantum mechanical theory in the following decades.
The eternal scientific question – so what?
By now, you are probably asking: what does all this discussion of quantum mechanics have to do with the conceptual journey that started with a simple mass on a spring? We began by examining a simple object oscillating on the end of a spring, then considered electrons sloshing back and forth through a circuit, and finally observed electric and magnetic fields oscillating into each other as they propagated in the form of light.
We now see that, on the quantum mechanical level, light itself is quantized. Just as the quantum satellite must emit a singular sonic boom instead of shoveling a continuum of air molecules out of its way, an electron must emit a singular burst of light instead of gradually radiating away its energy. This singular burst of light is called a photon.
Here is where we see our careful attention to analogy starts to pay off. In quantum physics, as in classical physics, a mass on a spring, electrons in a circuit, and light are all described by analogous mathematical expressions. Consequently, just as light is quantized into individual photons, the motions of electrons in circuits and masses on springs are also quantized under the right conditions. For example, when two oxygen atoms are bound together to form the diatomic 02 molecule, the atoms vibrate relative to each other, bouncing closer together then farther apart. This system can be described as two masses joined by a spring, and the atoms’ vibration is quantized just as we would expect.
Equivalent in an immediate, physical way
We can even go beyond this kind of conceptual link. Up to this point, we have talked about these various systems being equivalent in an abstract, mathematical sense; the equations look the same, so the systems should, with some variation, act the same.
When you quantize these systems, however, you can see that they can be equivalent in a much more immediate, physical way.
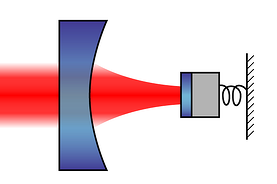
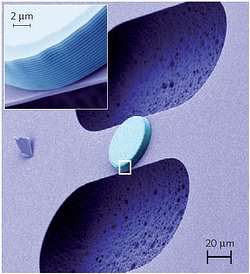
Quantum Optomechanics
One remarkable example is the field of quantum optomechanics, which explores the methods by which we can use light to manipulate tiny mechanical structures. In some optomechanics experiments, scientists fire photons at a mirror mounted on a spring. The mirror’s width is smaller than that of a human hair and it vibrates one million times each second, but it is nonetheless just a mass on spring. The scientists can fire a low-energy photon at the mirror and receive a high-energy photon in return. That extra energy comes from taking one quantum of vibration out of the spring. Using this method, they can pump vibration out of the spring and cool it, like your refrigerator pumps thermal vibration out of that leftover pizza to turn that warm mass of dough and sauce into a cold slice.
I sometimes find it amazing that we can take two systems that seem completely different – light bouncing off a mirror and a mass vibrating on a spring – and couple them so that energy can flow seamlessly from light to vibration and back.
Circuits and vibration
We can perform a similar feat with circuits and vibration. Imagine a circuit composed of a capacitor and inductor, like we described in our earlier post. Electrons will oscillate back and forth at a characteristic frequency. Now, make one plate of the capacitor flexible, so that it can bend and vibrate like a microscopic drum head. Although the experiment is tremendously difficult, the system is conceptually just as simple as that; the round object pictured above is the capacitor and the stripes are the loops of the inductor.
Just like in the mirror experiment, scientists can inject a tiny bit of oscillating current into the circuit and pull a tiny bit of current, which has a higher energy, back out. That energy difference again comes from a quantum of vibration that has been extracted from the vibrating capacitor plate. They can perform this process so effectively that all vibration is extracted from the capacitor plate. Every single quantum of vibration. The drum head could not, on a microscopic level, possibly be more still.
I’ll give a final example from my own research. We’ve discussed how electrons in atoms emit a flash of light, a photon, when they move to a lower energy level, just as our quantum satellite emits a sonic boom. It turns out that, in certain circumstances, an electron can literally emit both a photon and a tiny sonic boom. Just as the quantized bit of light is called a photon (“photo” = light, like “photograph” or “photosynthesis”), the quantized bit of sound is called a phonon (“phono” = sound, like “telephone” or “headphones”). If you put an atom inside some kind of crystal, like a diamond, and the atom’s electrons remain in discrete levels, like the discrete heights of our quantum satellite, then the electron can either shed its energy with a photon, a flash of light that we can see and measure; or with a phonon, a vibration that propagates through the diamond like the satellite’s sonic boom propagates through the atmosphere; or with both at once. Again, I find it remarkable that quantum mechanics allows us to blend all of these concepts together so seamlessly.
Oscillating on a spring: simple, yet complex
Over the past several posts, we have seen how a simple idea – a mass oscillating back and forth on a spring – emerges again and again in many diverse fields of physics. This simple object reappears, sometimes conceptually and sometimes quite literally, in place after place, from your first high school mechanics class; through courses on electronics, electricity, magnetism, and quantum mechanics; and right up to the cutting edge of modern physics research. As I described in my first post on the power of analogy in science, the discovery, refutation, and demonstration of conceptual links between seemingly different ideas has been fueling scientific progress from Newton, Maxwell, and Einstein to the latest issue of Nature.
Of course, make sure to pair these big conceptual ideas with actual facts and figure! But don’t view physics as a list of equations to be memorized, a jumble of nearly meaningless numbers and variables. View it as a collection of ideas that inform and reinforce each other, a multitude of variations on a small number of basic themes. If you try to take this view, if you actively try to connect what your teacher says in your next physics class with some other lesson you’ve learned this semester, then you will learn more material, with less effort and more enjoyment.

Comments