 To invest or to not invest? That is the question. Well, maybe not THE question, but it is a question that many investors and students of economics are asked each year.
To invest or to not invest? That is the question. Well, maybe not THE question, but it is a question that many investors and students of economics are asked each year.
What is present value?
When faced with a possible investment opportunity, economists use a conceptual tool to help them decide whether a rational person should invest (or not invest) in that opportunity. The conceptual tool is called “present value”, and it allows people to directly compare the value of the future payoffs of an investment to the present costs of that investment. This is done by converting the future nominal payoff of an investment into the present value - the value of the future dollars measured in today’s dollars.
How do you calculate present value?
In order to calculate the present value of an investment, first you have to know the interest rate. The interest rate is the percentage of an investment that is additionally paid back to the lender for allowing the borrower to take out a loan. For example, if a bank is offering a savings account with an interest rate of 2% per year, then by putting $100 in the bank (i.e. “lending” the bank $100) they will pay you back $2 (2% of $100) at the end of the year. The interest rate is important because it tells you how much an investment now will be worth in the future, and you can use this information to calculate how much future payoffs are worth in present value dollars. In the example above, if you know that the interest rate is 2% per year, then you know that $100 right now will be worth $102 in a year (and that $102 in a year is worth $100 right now).
To calculate the Present Value (PV) of a future payoff, you need the following formula:
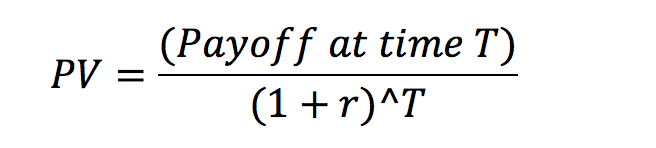
Where PV is the “Present Value” of an investment, “Payoff at time T” is the nominal value of the payoff of the investment that comes at a later time T, r is the interest rate, and T is how far in the future the payment comes. The interest rate r and time T should be calculated for the same time units. For example, if the interest rate is 2% per year, then T should be the number of years in the future that the payoff occurs. Continuing with the previous example, we can plug in the numbers: $102 from the bank 1 year from now when the interest rate is 2% gives us a present value of $100, just as expected.
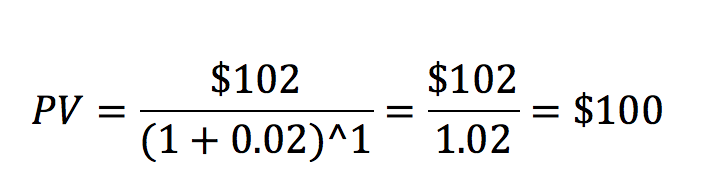
To demonstrate the wisdom of present value, imagine that you are an investor, and someone tells you that with a small cost of $1000 right now, they will give you $1200 in 10 years. (Also assume that the interest rate is 2% per year, like before.) Should you agree to this investment? To invest or to not invest??
At first glance, it seems to make sense - the payment you get in the future is $200 more than the cost of the investment, so you’ll earn $200 right? That’s true on the surface, but it doesn’t mean that this is a good investment. To know whether you should invest, you need to know how much $1200 in 10 years is worth right now. You need to know how much money you’d have to put in an account with 2% interest today in order to have $1200 in 10 years - in other words, you need to know the present value of the future payoff.
We can use the present value formula to figure out exactly that:
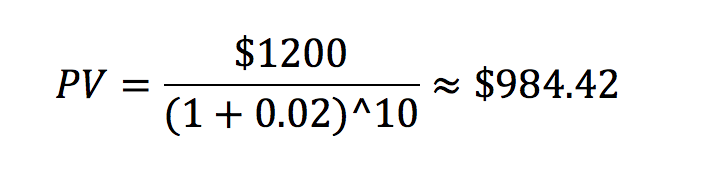
The present value formula shows that a $1200 payoff in 10 years is only worth about $984.42 in today’s money (i.e., you can get $1200 in 10 years by putting $984.42 in the bank and letting it gain interest). Since the present value of the investment is worth less than the cost of the investment ($984.42 is less than $1000), this indicates that the investor is offering you a bad deal - and it is better to not invest.
What happens if the interest rate changes? Because the interest rate determines how quickly money in the bank will grow, higher interest rates mean that the present value of payoffs in the future are going to be much lower. If you work it out, you’ll find that when the interest rate is 5% per year instead of 2% per year, the present value of the hypothetical $1200 payoff 10 years in the future is only worth about $736.70 in today’s dollars, much less than the $1000 current cost. On the other hand, when the interest rate is very low, it means that money in the bank grows slowly and therefore the present value of payments in the future will be higher. At an interest rate of 1% per year instead of 2% per year, the present value of a $1200 payoff 10 years in the future is actually worth $1086.34 in today’s dollars, which is higher than the present cost of $1000 for the investment (meaning that it’s a good investment and you should take the deal!)
By using this present value tool, economists and investors can determine the best places to put their money. In many cases, investments that sound good initially can end up being bad investments once the present value calculation is taken into account. By calculating the present value of future payments, one can directly compare this value to the present costs of the investments in order to make the optimal “invest or not invest” decision.
The original core team of economics tutors at Cambridge Coaching was drawn from the economics departments at Harvard and MIT, and the MBA programs at Harvard Business School and MIT’s Sloan School of Management. Our expanded team now includes doctoral candidates in economics at Columbia, NYU, and Princeton, as well as MBA candidates from the most selective programs.
We have deep experience teaching every economics topic at the high school, undergraduate, and graduate level. Many of our students come to us for help with the two foundational economics courses - microeconomics and macroeconomics - and we have tutors who have helped hundreds of students survive (and even enjoy) these notoriously difficult classes. Our tutors also work with graduate and MBA students on research and advanced coursework, including econometrics and impact evaluations. In short, whether you’re struggling with utility functions, or need help calculating a P-value, Cambridge Coaching has the tutor for you.
In all tutorials, we take a highly structured and personalized approach to ensure that our students receive the most effective and comprehensive tutoring available.
Curious to learn more about Economics? Check out some of our other posts below!

Comments